Analyse des données sur les microstructures d'otolithes

Stevenson et Campana – Chapitre 5 (PDF, 4.41 Mo)

Raccourcis vers les principales sections :

Introduction
Estimation de l'âge
Modèles de croissance
Modèles de croissance âge-température
Rétrocalcul de la croissance
Croissance et environnement
Analyse des dates d'éclosion
Estimation de la mortalité

L'information de la page doit être citée comme suit :

Campana, S.E., and C. M. Jones. 1992. Analysis of otolith microstructure data, p. 73-100. In D. K. Stevenson and S. E. Campana [ed.] Otolith microstructure examination and analysis. Can. Spec. Publ. Fish. Aquat. Sci. 117.

Introduction

La préparation et l'interprétation d'un otolithe ne constituent que la première étape de l'extraction de renseignements utiles sur un poisson. Comme on peut le comprendre, les difficultés techniques posées par l'examen des microstructures d'otolithes occupent une grande partie des heures de travail d'un chercheur. Pourtant, on porte souvent si peu d'attention à l'analyse des données obtenues qu'une grande partie des renseignements recueillis au prix de tant d'efforts est en réalité perdue. De fait, de nombreuses publications portant sur des données d'otolithes ne contiennent que l'information sur la taille selon l'âge, présentée parfois sous la forme d'un diagramme de dispersion, ignorant ainsi des renseignements souvent plus intéressants et utiles. Bien entendu, la plupart des analyses, même les plus simples comme les calculs de taux de croissance, nécessitent un échantillonnage complet et représentatif de toutes les cohortes ou de tous les stades du cycle biologique pertinents (voir Butler, dans la publication citée en haut de la page). Ce chapitre cherche à mettre en lumière les applications les plus utiles et les plus efficaces de l'examen des microstructures d'otolithes et ainsi inciter à analyser de manière plus complète et systématique les données sur les otolithes. De nombreuses analyses ne sont pas particulièrement difficiles à effectuer; il s'agit simplement de décider au préalable de la procédure à suivre. Dans les lignes qui suivent, nous présentons les méthodes qui nous semblent les plus adéquates pour aborder et effectuer chaque analyse, ainsi que des exemples dans la mesure du possible.

De nombreuses applications faisant appel à l'examen des microstructures d'otolithes ont des équivalents dans d'autres champs des sciences halieutiques. Parmi les exemples évidents, citons l'estimation de l'âge et du taux de croissance, tous deux étudiés depuis longtemps à l'échelle annuelle. Toutefois, une séquence type d'accroissements journaliers se prête beaucoup mieux à la plupart des applications que les annuli, en grande partie parce que la séquence de marques de chaque otolithe est plus longue et plus exacte sur le plan temporel. En outre, certaines applications, comme l'analyse des dates d'éclosion, se retrouvent presque seulement dans les études des microstructures d'otolithes. Sont passées en revue dans les lignes qui suivent les principales applications des données des microstructures d'otolithes, l'accent étant mis sur la discussion des analyses qui ne se retrouvent généralement pas dans d'autres domaines de recherche. Les simulations et la discussion sur l'analyse des dates d'éclosion sont nouvelles, car ce type d'analyse est encore en pleine évolution. La plus grande partie des autres renseignements ont déjà été présentés ailleurs, l'objectif étant de les réunir ici sous une forme cohérente, la plupart pour la première fois.

Estimation de l'âge

Conversion des dénombrements d'accroissements en estimations de l'âge

Soit un stade du cycle biologique d'une espèce pour laquelle la formation des accroissements journaliers a été validée (voir Geffen, dans la publication citée en haut de la page), leur nombre doit être proportionnel, mais pas nécessairement égal, à l'âge du poisson. Étant donné que le premier accroissement n'est pas obligatoirement formé à l'éclosion, des observations ou des essais doivent être réalisés pour déterminer l'âge auquel il s'est formé. Bien entendu, on peut commencer à dénombrer les accroissements à n'importe quel point de repère de l'otolithe auquel on peut attribuer un âge avec précision; il n'est pas nécessaire d'utiliser le premier accroissement ni la discontinuité d'éclosion. La marque formée à l&rsqrsquo;ouverture de la bouche est un exemple d'autre point de repère (Lagardère et Chaumillon 1988). Indépendamment du point utilisé, l'âge est calculé comme étant la somme de l'âge au moment de la formation du point de repère et du nombre d'accroissements présents après ce point. Bien que la détermination de l'âge d'un poisson soit habituellement l'objectif de l'examen de la microstructure de ses otolithes, chaque accroissement peut aussi être interprété pour obtenir sa date de formation si l'on connaît la date de capture (= date de formation du dernier accroissement ou accroissement marginal). Les accroissements datés se révèlent de plus en plus utiles pour les analyses de corrélation entre les facteurs environnementaux et la séquence de croissance des otolithes (p. ex., Methot 1981; Campana et Hurley 1989; Suthers et al. 1989).

L'estimation de l'âge par dénombrement des accroissements journaliers est simple en principe, mais dans la pratique, les erreurs et les incertitudes inhérentes à l'examen de microstructures la compliquent (voir Neilson ainsi que Campana, dans la publication citée en haut de la page). Dans une certaine mesure, les incertitudes dans la détermination de l'âge peuvent être revues à la baisse si plusieurs otolithes sont examinés. Tous les téléostéens ont trois paires d'otolithes, dont deux paires interprétables la plupart du temps. Étant donné que les erreurs de dénombrement des accroissements sont au moins en partie imputables à des artéfacts de préparation, l'examen des deux otolithes d'une paire donnée peut aider à réduire la variance (c.-à-d. à accroître la précision) de chaque estimation d'âge. Lorsque l'on peut démontrer que d'autres types d'otolithes renferment la même information sur l'âge (ou peuvent être étalonnés au même âge), on peut lire plusieurs paires d'otolithes pour plus de précision (Campana et Hurley 1989). Bien entendu, les particularités de la microstructure des otolithes imputables à la croissance du poisson se reflètent dans tous les otolithes et il est peu probable que plusieurs lectures permettent de réduire cette source d'erreur. Il faut aussi noter que les lectures de plusieurs otolithes d'un même poisson n'équivalent pas au même nombre de lectures d'un seul otolithe; ces dernières permettent de réduire la variance imputable aux erreurs de dénombrement tandis que les premières permettent de réduire la variance due aux erreurs de dénombrement et aux défauts de préparation.

Quand cela est possible, des lectures multiples de plusieurs otolithes d'un poisson donné donnent la meilleure estimation de son âge. Toutefois, une moyenne globale de tous les dénombrements est rarement le résultat qui convient. Il est préférable d'adopter une procédure d'estimation de l'âge qui comprend : (1) l'établissement de la « meilleure » estimation du nombre d'accroissements pour chaque otolithe, (2) le regroupement du nombre d'accroissements pour chaque type d'otolithe, (3) la conversion de ce total en estimation de l'âge et (4) le regroupement des résultats pour tous les types d'otolithes. C'est, en théorie du moins, la procédure la plus appropriée. Cependant, en pratique, le temps et les efforts nécessaires à la lecture de plusieurs otolithes d'un seul poisson doivent être soupesés par rapport aux avantages offerts par l'examen d'un nombre plus grand de poissons. Empiriquement, l'examen de deux otolithes (habituellement d'un seul type) de chaque poisson semble être un bon compromis entre la précision concernant le poisson étudié et la taille globale de l'échantillon.

La « meilleure » estimation du nombre d'accroissements sur un otolithe donné peut être la moyenne de plusieurs dénombrements si l'on considère que leur fiabilité est égale. L'utilisation d'une médiane, plutôt que d'une moyenne, réduit les effets d'un dénombrement anormal. Toutefois, étant donné que, généralement, les lecteurs d'otolithes accordent plus de crédit à certaines lectures, une forme de pondération selon la fiabilité est souvent préférée. La pondération peut se faire comme suit ou être légèrement plus subjective par le choix d'un seul dénombrement, qui est considéré comme le plus fiable. Dans la plupart des cas, la différence entre les deux méthodes de pondération est minime. Après avoir attribué un seul nombre d'accroissements à chaque otolithe, on établit une valeur unique pour chaque type d'otolithe, en calculant la moyenne ou la moyenne pondérée. On convertit ensuite le nombre d'accroissements pour chaque type d'otolithe en estimation de l'âge à l'aide de la formule de conversion appropriée (p. ex., âge = nombre d'accroissements sur le lapillus + 2). En dernier lieu, on calcule la moyenne (pondérée ou non) du nombre d'accroissements pour tous les types d'otolithe. L'algorithme mathématique pour obtenir le meilleur nombre d'accroissements (C_tj) provenant du j ^e (premier ou deuxième) otolithe de type t (p. ex., sagitta, lapillus ou asteriscus) est le suivant :

(1)

C_{t j} = \frac{(\sum_{1}^{R} X_{i} ⨯ W_{i})}{\sum_{1}^{R} W_{i}}

où R représente le nombre de fois que l'otolithe a été lu et Wi le poids donné à chaque dénombrement (X_i). Bien que les poids statistiques soient souvent calculés comme l'inverse de la variance, il n'y a aucune variance associée à un seul dénombrement. Il est plus utile dans ce cas-ci de pondérer en fonction de la confiance accordée au dénombrement, par exemple en adoptant une échelle arbitraire allant de 1 (peu fiable) à 5 (dénombrement sans ambiguïté) pour chaque otolithe. Le calcul du nombre moyen d'accroissements pour un type d'otolithe donné est une simple variante de l'équation (1) où soit un coefficient de pondération est attribué à chaque otolithe selon le degré de confiance, soit les facteurs de pondération sont considérés comme égaux, ce qui donne une moyenne simple. Après avoir converti chacun des dénombrements pour le type d'otolithe donné en estimations de l'âge, on calcule la moyenne finale (pondérée) pour tous les types d'otolithes. Il est important de noter que cette méthode, qui permet de calculer des moyennes (pondérées) à chaque étape, n'équivaut pas à une moyenne (pondérée) de toutes les lectures regroupées. Pour ce qui est de l'utilisation de moyennes pondérées, la pondération semble être plus importante aux deux premières étapes (calcul du meilleur nombre d'accroissements pour chaque otolithe et type d'otolithe). À moins qu'un type d'otolithe soit clairement supérieur aux autres, une moyenne simple pour tous les types d'otolithe suffit selon toute probabilité.

Prenons l'exemple suivant, reposant sur trois lectures de deux sagittae et d'un lapillus (le second lapullus prévu ayant été perdu lors de la préparation). On attribue un niveau de confiance à chaque lecture, allant de 1 (peu fiable) à 5 (grande fiabilité) et on suppose que les dénombrements ont débuté à une discontinuité formée un jour après l'éclosion :

Envisageons l'exemple suivant, basé sur trois lectures chacune de deux sagittas et d'un lapillus (un lapillus a été perdu pendant la préparation). Les niveaux de confiance ont été attribués sur une échelle de 1 (confiance faible) à 5 (confiance élevée). Supposons que le dénombrement des incréments a débuté lors d'un contrôle qui s'est formé un jour après l'éclosion :
	Nombre	Niveau	Nombre	Niveau	Nombre	Niveau	Moyenne pondérée
Sag 1	20	5	18	4	28	1	20.0
Sag 2	22	4	23	3	19	4	21.2
Lap 1	19	4	20	4	21	4	20.0

En supposant que la facilité d'interprétation de Sag 1 et de Sag 2 était semblable, on obtient un nombre moyen d'accroissements Sag de 20,6. On convertit ensuite les dénombrements Sag et Lap en âges (nombre d'accroissements + 1) et on en calcule la moyenne, ce qui donne un âge estimé à 21,3 j. On constate une différence entre cette estimation et la moyenne simple de toutes les lectures (= 21,1 + 1 = 22,1 j). Il faut aussi noter que le même poids a été attribué aux types d'otolithes dans le calcul de l'âge final estimé bien que deux sagittae aient été lues, mais seulement un lapillus. Une pondération égale convient si la facilité de préparation et/ou d'interprétation des deux types d'otolithes diffère, mais que rien ne permet de considérer un type comme plus fiable que l'autre. Lorsqu'un type est jugé plus fiable que l'autre, il est probablement préférable de déterminer l'âge de la paire fiable seulement.

Exactitude et précision

Les estimations de l'âge sont plus utiles lorsqu'elles sont exactes et précises. En revanche, une estimation exacte n'a pas besoin d'être précise et inversement (Campana et Moksness 1991). L'exactitude désigne la proximité de l'estimation par rapport à la « vraie » valeur, tandis que la précision indique la reproductibilité de chaque mesure. Ainsi, un âge moyen peut être exact (proche de la vérité) malgré l'imprécision des observations individuelles (qui varient grandement). Inversement, et cela est souvent le cas dans les études de détermination de l'âge, les estimations de l'âge peuvent être précises (hautement reproductibles, par un ou plusieurs lecteurs) mais pas nécessairement exactes. Les tests d'exactitude exigent un moyen indépendant et absolu de détermination de l'âge (voir Geffen, dans la publication citée en haut de la page); par exemple, l'exactitude n'est pas démontrée si les estimations de l'âge provenant d'otolithes et de vertèbres concordent. Les indices de précision, susceptibles de fournir de l'information utile sur les sources d'erreur dans une étude de détermination de l'âge, sont par ailleurs faciles à calculer. Ces indices sont couramment appliqués dans les comparaisons entre résultats de différents lecteurs et méthodes de détermination de l'âge (Secor et Dean 1989). Ils peuvent en outre servir à jauger la difficulté relative à établir l'âge de différentes espèces et à rejeter les échantillons de fiabilité douteuse (Secor et Dean 1989; Schultz 1990).

Les indices de précision classiques sont peu utiles pour les études des microstructures d'otolithes et en tout cas, sont aussi passés de mode dans les études de détermination de l'âge reposant sur les annuli. Plus précisément, les mesures du pourcentage de concordance varient considérablement d'une espèce à l'autre et d'un âge à l'autre chez une espèce. Beamish et Fournier (1981) illustrent cette réalité en faisant remarquer qu'un niveau de concordance de 95 % à un an près entre deux lecteurs d'âge de la morue du Pacifique ( Gadus macrocephalus) indique un faible niveau de précision étant donné le nombre dérisoire de classes d'âge pêchées. D'un autre côté, un niveau de concordance de 95 % sur une période de cinq ans représente un niveau élevé de précision pour l'aiguillat commun ( Squalus acanthias), en raison de sa longévité (60 ans). Beamish et Fournier (1981) recommandent donc d'utiliser le pourcentage moyen d'erreur (PME), défini comme suit :

(2)

100 % ⨯ \frac{1}{R} \sum_{i = 1}^{R} \frac{| X_{i j} - X_{j} |}{X_{i}}

où Xij est la i ^e détermination de l'âge du j ^e poisson, Xj l'âge moyen du j ^e poisson et R le nombre de fois que l'on donne un âge à chaque poisson. La moyenne obtenue pour de nombreux poissons est l'indice de PME. Chang (1982) convient que le PME représente une nette amélioration par rapport au pourcentage de concordance, mais il suggère d'utiliser un écart type dans l'équation (2) plutôt que l'écart absolu de l'âge moyen. L'équation qui en résulte donne une estimation du coefficient de variation (CV) et contrairement à l'équation (2), ne suppose pas que l'écart type est proportionnel à la moyenne. Le CV est exprimé comme le rapport entre l'écart type et la moyenne, comme suit :

(3)

100 % ⨯ \frac{\sqrt{\sum_{i = 1}^{R} \frac{{(X_{i j} - X_{j})}^{2}}{R - 1}}}{X_{j}}

L'équation (3) est le CV de l'estimation de l'âge d'un seul poisson (j ^e poisson). Comme dans le cas de l'équation (2), on peut calculer le CV moyen pour tous les poissons. Les équations (2) et (3) donnent des valeurs comparables pour ce qui est de la précision (Chang 1982); toutefois, en raison de l'absence de proportionnalité théorique entre l'écart type et la moyenne, cette dernière est statistiquement plus rigoureuse et donc plus souple. L'indice de variation proposé par Lai et al. (1987) est probablement le même que l'équation (3), bien qu'il semble y avoir une coquille dans sa présentation. Chez certaines espèces, le PME et le CV diminuent avec l'âge jusqu'au stade juvénile, ce qui indique la difficulté relative à établir précisément l'âge de très jeunes larves (p. ex., Savoy et Crecco 1987; Campana et Moksness 1991). Il est aussi important de noter que le PME et le CV diminuent avec l'âge, même si l'erreur absolue du nombre demeure constante. Par exemple, une variabilité du nombre de ± l chez une larve de 10 j correspond à un CV d'environ 9 %, alors que la même variabilité chez une larve de 1 j aboutit à un CV de près de 90 %. Par conséquent, il est impossible de comparer la précision des âges entre deux groupes si ceux-ci affichent des distributions des âges sensiblement différentes.

Clés âge-longueur

La détermination de l'âge d'un grand nombre de poissons, que ce soit au niveau journalier ou annuel, nécessite presque invariablement une forme quelconque de sous-échantillonnage. Étant donné qu'il est de loin plus facile de mesurer la longueur d'un poisson que de déterminer son âge, on peut se servir du sous-échantillonnage pour estimer l'âge d'un grand nombre de poissons dont on ne connaît que la longueur à partir d'un petit échantillon dont on connaît l'âge et la longueur. On calcule l'âge moyen selon la longueur par régression inverse d'une courbe de croissance linéaire, puis on l'applique à un échantillon de poissons de longueur connue (Bolz et Lough 1988). Toutefois, comme cette méthode ignore la variabilité inhérente de la taille selon l'âge, elle ne peut être utilisée que pour les applications les plus générales. Les clés âge-longueur, qui sont essentiellement des tableaux de contingence de catégories d'âge par catégories de longueur, renferment plus de renseignements sur l'âge et la longueur et sont donc couramment utilisées pour les pêches commerciales. Nombreuses sont les études publiées sur l'utilisation et l'abus de ces clés (Kimura 1977; Westrheim et Ricker 1978; Doubleday et Rivard 1983), mais elles ne seront pas abordées ici. Une hypothèse importante sous-tendant l'utilisation appropriée des clés âge-longueur est qu'elles sont tirées d'une même population, prélevée au même moment à un seul endroit, comme les grands échantillons de fréquence des longueurs. Étant donné que de graves erreurs peuvent être commises si cette hypothèse est ignorée, les clés âge-longueur ne seront généralement pas applicables d'une saison, d'une année, d'une population ou d'un milieu à l'autre.

Le plus souvent, les clés âge-longueur sont élaborées selon l'une des deux méthodes décrites ici. Les deux approches reposent sur un échantillonnage en deux étapes (Cochran 1963), pour lequel un grand échantillon de fréquences de longueur est sous-échantillonné aux fins de détermination de l'âge. Le sous-échantillonnage se fonde sur un échantillon aléatoire de l'échantillon de fréquences de longueur ou est stratifié selon la catégorie de longueur (p. ex., l'âge d'un échantillon aléatoire de chaque catégorie de longueur est évalué). La stratification fondée sur la longueur est généralement privilégiée, car elle évite le problème de la sous-représentation des poissons âgés, qui sont moins abondants (Fournier 1983). La taille des sous-échantillons de chaque catégorie de longueur peut être fixe ou proportionnelle au nombre de poissons de cette catégorie de longueur (Kimura 1977). Quelle que soit la méthode adoptée, il est important que la plage des catégories de longueur dans la clé couvre la même plage que celle observée dans l'échantillon des longueurs.

Prenons l'exemple simple suivant, dans lequel une clé âge-longueur dérivée d'un petit sous-échantillon est utilisée pour ventiler un grand échantillon de fréquences de longueur (FL) :
Catégorie de longueur	Catégorie d'âge						Somme	FL
Catégorie de longueur	5	6	7	8	9	10	Somme	FL
10	2	-	-	-	-	-	2	20
12	1	3	2	-	-	-	6	30
14	-	2	7	5	1	-	15	50
16	-	-	2	4	3	1	10	40
Sum	3	5	11	9	4	1	33	140

Le vecteur FL est multiplié par la proportion selon l'âge dans chaque catégorie de longueur, ce qui donne :
Catégorie de longueur	Catégorie d'âge						Somme
Catégorie de longueur	5	6	7	8	9	10	Somme
10	20	-	-	-	-	-	20
12	5	15.0	10.0	-	-	-	30
14	-	6.7	23.3	16.7	3.3	-	50
16	-	-	8.0	16.0	12.0	4	40
Somme	25	21.7	42.3	32.7	15.3	4	140

Les comparaisons des longueurs selon l'âge reposent ordinairement sur des tests paramétriques, bien qu'il existe des équivalents non paramétriques pour la plupart des tests à deux échantillons. Si la relation entre la longueur et l'âge est linéaire (ou peut être transformée pour le devenir) et étant donné les autres hypothèses d'une analyse de variance (ANOVA), une analyse de covariance (ANOCOVA) peut étudier très efficacement les différences entre échantillons (p. ex., Secor et Dean 1989; Thorrold et Williams 1989). Il faut toutefois noter qu'une ANOCOVA pour deux échantillons n'équivaut pas nécessairement à un test t de la pente des droites de régression des deux échantillons. La comparaison des pentes suppose que leurs points d'intersection sont semblables; s'ils ne le sont pas, il peut être difficile d'interpréter les différences entre les pentes. L'ANOCOVA se prête mieux à l'étude de ce type de problème.

Dans toutes les analyses statistiques, tout particulièrement celles mentionnées ci-dessus, il est important de considérer la signification et l'efficacité statistiques avant de tirer des conclusions. La signification statistique, soit la probabilité que l'hypothèse nulle soit rejetée (aucune différence) lorsqu'il existe en fait une différence, est communément comprise. Ainsi, les différences statistiquement significatives des échantillons sont généralement faciles à interpréter. Toutefois, les différences non significatives peuvent être dues à une similarité réelle entre les échantillons ou à une faible efficacité statistique. Cette dernière peut résulter de la faible taille de l'échantillon ou de la variabilité élevée des données, entre autres choses, ce qui peut dissimuler une différence réelle entre les échantillons. Rien ne permet donc de conclure ni même de suggérer qu'il n'y a aucune différence entre les échantillons à moins de démontrer que l'efficacité statistique est élevée. Les analyses de faible efficacité statistique sont répandues et leurs inférences ont souvent masqué la réalité (Rice 1987; Peterman 1990).

Estimation de l'âge par intégration numérique de largeurs d'accroissements journaliers

Jusqu'à maintenant, la discussion a essentiellement porté sur l'estimation de l'âge des jeunes poissons, principalement les larves et les juvéniles. Bien que quelques chercheurs aient tenté, avec plus ou moins de succès, de déterminer l'âge d'adultes en dénombrant les accroissements journaliers (Pannella 1971; Brothers et al. 1976; Radtke 1984), on admet généralement que les otolithes des adultes sont difficiles et fastidieux à préparer et à interpréter. Outre la possibilité que la formation des accroissements journaliers devienne intermittente chez les poissons âgés lorsque la croissance somatique ralentit (Campana et Neilson 1985), les problèmes logistiques rencontrés lors de la préparation d'un otolithe volumineux aux fins d'examen de sa microstructure peuvent rendre impossibles à interpréter de longues séquences d'accroissements journaliers. Lorsqu'il semble exister un patron d' annuli, le dénombrement des accroissements journaliers présents entre le noyau et le premier annulus permet de confirmer la nature de ce dernier (Victor et Brothers 1982; Morales-Nin 1988). Cependant, l'identification des annuli suivants demeure problématique. Malgré les problèmes d'interprétation de la microstructure des otolithes d'adultes, dans les cas où les annuli sont ambigus ou absents (p. ex., chez de nombreuses espèces tropicales) et en particulier si une autre méthode de détermination de l'âge est aussi utilisée (comme une analyse des fréquences des longueurs), une forme quelconque de détermination de l'âge otolithaire peut présenter de grands avantages. En tenant compte de ces mises en garde, Ralston et Miyamoto (1983) ont mis au point une méthode reposant sur le sous-échantillonnage des largeurs des accroissements journaliers d'un otolithe d'adulte et la mesure de ces largeurs dans les sections interprétables du radius. Dans le contexte de la relation entre la largeur des accroissements, la largeur des sections interprétables et la distance les séparant du nucleus, l'interprétation des données intégrées contribue à déterminer l'âge quotidien d'un otolithe d'une taille donnée. L'utilisation d'une relation prédictive entre la taille d'un otolithe et la longueur d'un poisson permet ensuite d'estimer sa longueur selon l'âge. Bien que critiquable en cas de longues interruptions de la croissance des otolithes, cette méthode permet de contourner les problèmes que posent les séquences d'accroissements mal définis et d'améliorer l'efficacité et la productivité du dénombrement de tous les accroissements.

Ralston et Williams (1989) décrivent en détail la méthode de l'intégration numérique. Elle consiste essentiellement à d'abord examiner la coupe préparée d'un otolithe le long d'un axe prédéfini entre le noyau et le bord pour trouver des séquences non ambiguës d'accroissements journaliers. À des intervalles fréquents mais arbitraires, on détermine leur largeur moyenne en mesurant la longueur axiale d'un petit nombre successif d'entre eux (~ 10-20), puis on divise cette valeur par le nombre d'accroissements journaliers compris dans cette séquence. En mesurant aussi la distance entre le milieu de la séquence d'accroissements et le nucleus, on peut estimer la largeur moyenne des accroissements sur un radius donné de l'otolithe. Cette valeur peut ensuite servir à calculer le taux instantané de croissance de l'otolithe.

Pour estimer l'âge, Ralston et Williams (1989) ont subdivisé les longueurs des otolithes, à partir du nucleus, en intervalles de 500 µm. Le choix de cet intervalle était arbitraire et pouvait être modifié selon l'espèce étudiée. Ils ont ensuite calculé le taux moyen de croissance des otolithes pour chaque intervalle de 500 µm d'après le nombre de séquences d'accroissements comprises dans cet intervalle. Puis, ils ont divisé le taux de croissance pour chaque intervalle (exprimé en µm) par 500 µm afin d'estimer le nombre de jours nécessaires pour compléter la croissance dans cet intervalle. Ils ont ensuite divisé la somme de ces résultats (en jours) pour chaque poisson par 365 pour obtenir une estimation de l'âge (en années). Enfin, ils ont entré cet âge estimé et la longueur observée de chaque poisson dans l'un des modèles de croissance courants. En général, on obtient de meilleures estimations non biaisées du taux de croissance en n'entrant qu'une seule valeur âge-longueur par poisson. Toutefois, lorsque la quantité de données est limitée, on peut utiliser la relation générale poisson-otolithe afin de rétrocalculer la longueur du poisson pour la taille de l'otolithe correspondant à la fin de croissance à chaque intervalle de 500 µm. L'âge du poisson à ces mêmes points peut être obtenu par la méthode décrite ci-dessus. On dispose ainsi de plusieurs estimations de la longueur selon l'âge pour chaque poisson, qui peuvent ensuite toutes être entrées dans un modèle de croissance. Cependant, les observations multiples réalisées sur un seul poisson ne sont pas indépendantes.

La méthode d'estimation de l'âge annulaire par intégration numérique suppose que la formation des accroissements journaliers est continue pendant toute la vie du poisson. Il est en effet peu probable que de courtes périodes d'interruption de la croissance des otolithes réduisent notablement l'exactitude des calculs. La possibilité que la largeur des accroissements journaliers s'atténue avec l'âge au point qu'il soit difficile de la mesurer est plus préoccupante. Dans ce cas, aucun accroissement formé chez un poisson âgé ne serait mesurable et les taux de croissance correspondants de l'otolithe se fonderaient sur les périodes précédentes de croissance rapide. Les âges calculés seraient alors des sous-estimations de l'âge réel du poisson. Bien que la largeur des accroissements chez les otolithes d'adultes ait rarement été mesurée, il est inquiétant de constater que Ralston et Williams (1989) se sont heurtés à la même difficulté en examinant des otolithes de colas bagnard ( Pristipomoides zonatus). Ils n'ont, par conséquent, pas pu mesurer la largeur des accroissements d'otolithes au diamètre supérieur à 7 500 µm, ce qui était le cas des otolithes de la plupart des colas bagnards visés par la pêche. Ces chercheurs étaient extrêmement confiants dans leurs estimations de l'âge des petits individus, mais il leur a été impossible d'évaluer l'erreur d'estimation pour l'âge des gros poissons.

Une deuxième hypothèse sous-tendant la méthode d'intégration numérique veut que les séquences d'accroissements mesurés représentent, sans biais, l'intervalle d'otolithe correspondant. Les artéfacts de préparation qui rendent moins visibles les accroissements de certaines sections ne devraient donc pas poser problème. Toutefois, Ralston et Williams (1989) recommandent de s'assurer que les séquences d'accroissements sont choisies aussi objectivement que possible et non d'après la largeur des accroissements et la facilité à les interpréter qui en résulte.

Modèles de croissance

L'élaboration d'un modèle de croissance paramétré est souvent considérée comme un produit normal de l'examen des microstructures d'otolithes. La complexité des modèles de croissance varie; ils vont de la simple régression linéaire de la longueur du poisson par rapport au nombre d'accroissements à des estimations perfectionnées de vraisemblance maximale de la longueur selon l'âge. Dans la plupart des cas, le modèle est conçu pour prédire la longueur moyenne ou le taux de croissance probable à un âge donné et/ou faciliter la comparaison entre la croissance estimée et d'autres estimations publiées. De nombreux modèles excluent les renseignements sur la variance observée de la longueur selon l'âge. Pour cette raison, un diagramme de dispersion simple de la longueur en fonction de l'âge est un point de départ judicieux pour toute analyse de la croissance.

En principe, les calculs du taux de croissance devraient se fonder sur les trajectoires de croissance de poissons individuels, mais en pratique, les trajectoires des populations sont souvent considérées comme représentant la croissance des individus malgré le biais potentiel introduit par la mortalité sélective selon la taille et l'évitement des engins (Ricker 1975). Toute mesure de la taille d'un poisson est valable dans les calculs, mais nous n'utiliserons ici que sa longueur. Il existe aussi plusieurs mesures du taux de croissance. Les plus connus sont le « taux absolu de croissance », défini comme le changement de longueur (ou de poids) d'un poisson par intervalle de temps, et le « taux instantané de croissance », où l'intervalle de temps est réduit à une valeur proche de zéro et le taux de croissance est calculé comme une proportion de la taille initiale du poisson (Ricker 1979). Il est important de noter que le taux absolu de croissance varie en fonction de l'intervalle de temps choisi si la croissance n'est pas linéaire. Pour cette raison, le taux instantané absolu de croissance, ou la tangente à la pente de la courbe de croissance selon l'âge à l'âge désiré, est parfois une mesure plus significative de la croissance que le taux absolu de croissance.

Les calculs du taux de croissance peuvent reposer sur des équations issues soit de courbes empiriquement ajustées soit de certains modèles de croissance généralement acceptés. En fait, la distinction entre les deux est quelque peu arbitraire. Les modèles de croissance les plus souvent utilisés (p. ex., modèles de régression linéaire, de Gompertz, logistique et de von Bertalanffy) présentent l'avantage de faciliter l'interprétation des estimations des paramètres connexes par d'autres chercheurs. Toutefois, lorsque les modèles ci-dessus ne peuvent pas être ajustés, il ne faut pas hésiter à utiliser des courbes empiriquement ajustées.

Modèles empiriques

De très nombreuses méthodes empiriques d'ajustement des courbes sont applicables aux données de croissance (Lancaster et Salkauskas 1986). Les méthodes de lissage généralement associées à l'analyse de séries chronologiques de données peuvent donner des mesures utiles de la tendance centrale, mais elles ne se prêtent pas toutes au calcul du taux de croissance. La méthode de lissage non linéaire robuste (plus communément appelé lissage médian) est une technique non paramétrique, relativement peu sensible aux valeurs aberrantes des données. La méthode paramétrique analogue est le lissage par moyenne mobile. Les deux méthodes permettent de calculer la médiane (ou la moyenne) d'un nombre choisi de points de part et d'autre d'un point cible. Si cela est jugé nécessaire, les points peuvent être pondérés en fonction de leur proximité avec ce dernier. Les courbes lissées par médiane et moyenne mobile permettant un ajustement acceptable d'une série de données simulées sur la longueur selon l'âge (figure 1), elles conviennent pour le résumé des tendances de la longueur selon l'âge. On doit toutefois noter que ni l'une ni l'autre de ces méthodes ne donnent une équation permettant de calculer le taux de croissance. Au besoin, on peut obtenir une approximation du taux de croissance selon l'âge en calculant la pente de la tangente à la courbe à l'âge désiré. L'étude de Brothers et McFarland (1981) est un exemple de l'application de moyennes mobiles à des données de croissance.

Exemples de méthodes de lissage paramétrique et non paramétrique appliquées à une série de données simulées concernant la longueur selon l'âge. Les méthodes paramétrique (relissage par moyenne mobile sur 10 termes) et non paramétrique (lissage par médiane 5RSSH) permettent d'ajuster suffisamment ces données, mais ni l'une ni l'autre ne donnent d'équations descriptives.

Les régressions polynomiales peuvent efficacement résumer des données de longueur selon l'âge, d'autant qu'elles incluent une équation descriptive qui peut servir à calculer le taux instantané de croissance. Les régressions polynomiales adoptent la formule générale suivante :

(4)

L = a + b_{1} X + b_{2} X^{2} + b_{3} X^{3} + ... + b_{n} X^{n}

où a et b₁ ... b_n sont les paramètres de régression à estimer (généralement à l'aide de la méthode des moindres carrés), L est la longueur (ou le poids) du poisson et X est l'âge ou le nombre d'accroissements. Le nombre de termes (n) entrés doit être supérieur de un au nombre de points d'inflexion de la courbe qui dépasse rarement quatre dans la plupart des courbes de croissance. À titre d'exemple de lissage polynomial, est présentée à la figure 2 une régression polynomiale de troisième ordre appliquée aux données simulées de la figure 1. Wilson et Larkin (1982), West et Larkin (1987), ainsi que McMichael et Peters (1989), ont appliqué des régressions polynomiales à des données sur les otolithes.

Exemple d'une régression polynomiale appliquée aux mêmes données sur la longueur selon l'âge que dans la figure 1. L'utilisation d'une régression de troisième ordre a produit deux points d'inflexion dans la courbe ajustée. Bien que la régression polynomiale soit souvent considérée comme une courbe ajustée empiriquement, l'équation de régression qui lui est associée peut servir à des fins prédictives.

Modèles de régression linéaire simples

Bien que la distinction entre les courbes empiriques de la longueur selon l'âge et les modèles de croissance soit quelque peu arbitraire, les régressions linéaires simples sont l'un des modèles dits de croissance le plus souvent appliqués (p. ex., Geffen 1982; Walline 1985; Leak et Houde 1987; Victor 1987). Elles prennent la forme suivante :

(5)

L = a + b X

Les régressions linéaires (figure 3) sont faciles à ajuster et à interpréter et se prêtent bien au calcul de l'intervalle de confiance de la pente b (taux de croissance) et de valeurs ponctuelles. Bien qu'elles soient généralement appliquées à des périodes de croissance relativement courtes, pendant lesquelles même les régimes de croissance intrinsèquement curvilignes peuvent sembler linéaires, elles peuvent aussi être appliquées à une période ayant connu un taux de croissance constant.

Exemples de l'application d'une régression linéaire simple et d'une régression par moyenne géométrique à une série de données simulées de longueur selon l'âge. Les pentes des deux régressions deviennent de plus en plus semblables au fur et à mesure que la corrélation entre la longueur et l'âge augmente.

Pour obtenir une ligne droite, la régression linéaire peut être remplacée par une régression fonctionnelle ou régression par moyenne géométrique [MG] (Ricker 1973, 1984), où

(6)

Y = U + v X

et la pente (v) est le rapport des écarts-types (s) ou la racine carrée de la somme des écarts de Y et X mis au carré (somme des carrés), comme suit :

(7)

v = \pm \frac{S_{y}}{S_{x}} = \sqrt{\frac{{SS}_{y}}{{SS}_{x}}}

Ricker (1973, 1984) suggère d'appliquer la régression par MG lorsque la variabilité de X et de Y (non mesurée) est inhérente ou lorsque la distribution de ces variables n'est pas normale. Bien qu'il présente des exemples d'emploi de la régression à des fins de prévision, sa principale application reste la description, où aucune des variables n'est clairement déterminante (p. ex., la longueur par rapport au poids). Ce serait dépasser l'objet du chapitre que de décrire en détail les avantages et les inconvénients des régressions fonctionnelles. Contentons-nous d'indiquer que la valeur relative des régressions par MG en matière de recherche halieutique est quelque peu controversée (Sprent et Dolby 1980; Jensen 1986). Les principaux inconvénients concernent les hypothèses de distribution de l'erreur et l'absence de valeurs statistiques significatives pour l'estimation de la pente. La pente de la régression par MG semble toutefois une mesure de la tendance centrale (relation fonctionnelle) aussi bonne qu'une autre et peut-être meilleure que celles issues de régressions prédictives. Dans le cadre des modèles de croissance des otolithes, l'utilité des régressions par MG semble limitée, car la plupart des modèles de croissance sont ajustés de sorte à pouvoir prédire la longueur d'après l'âge et les régressions prédictives conviennent mieux à cette tâche (Jensen 1986). En outre, les données de dénombrement des accroissements journaliers, généralement considérés comme la variable indépendante dans une régression âge-longueur, peuvent souffrir d'un niveau élevé d'erreur de mesure. Ricker (1973, 1984) déconseille justement d'utiliser une régression fonctionnelle en cas d'erreur dans la mesure de la variable indépendante. Bien que certains chercheurs aient appliqué des régressions par MG à des données poisson-otolithe (Gjosaeter 1987; Watanabe et al. 1988), personne encore, pour autant que nous le sachions, ne l'a fait pour des données âge-longueur. Quoi qu'il en soit, les régressions par MG ressemblent de plus en plus à des régressions simples à mesure que la corrélation entre les variables X et Y augmente. Une comparaison des deux types de régressions, reposant sur des données simulées, est présentée à la figure 3.

Modèles de croissance curviligne

Les modèles de croissance curviligne conviennent généralement bien à la description de la croissance des jeunes poissons, en particulier des larves. Le choix de modèles est vaste, mais aucun ne convient à tous les stades du cycle biologique de toutes les espèces (Ricker 1979). Le principal avantage de ce type de modèle est leur souplesse, qualité nécessaire pour tenir compte des courbes de croissance en S caractéristiques de la plupart des jeunes poissons. Un certain nombre de ces modèles de croissance a été élaboré au départ à partir de processus de croissance perçus, qui n'ont jamais été fermement corroborés. Le choix d'un modèle de croissance curviligne approprié repose donc généralement sur la qualité de l'ajustement et la commodité (Ricker 1979). À la lumière de ces critères, ainsi que de la connaissance et de l'acceptation générale dont ils sont l'objet, les modèles exponentiel, de Gompertz, logistique et de von Bertalanffy seront brièvement abordés. Pour obtenir une description plus complète de ces modèles et d'autres modèles de croissance, voir les excellentes évaluations de Ricker (1979) et de Brett (1979).

Les courbes exponentielles sont les analogues curvilignes de la régression linéaire simple discutée ci-dessus, soit :

(8)

L = {a e}^{G X} = a exp [G X]

ou l'équivalent

(9)

L = exp [a^{'} + G X]

où a et exp(a') sont la longueur du poisson à l'âge 0 et G est le taux instantané de croissance. Le taux absolu de croissance (g) à un âge donné est la dérivée de l'équation (8), soit :

(10)

gx = a G exp [G X]

Étant donné que l'on peut ajuster une courbe exponentielle à l'aide d'une simple régression linéaire après transformation logarithmique des données de longueur, les deux types de modèles présentent les mêmes avantages statistiques. Une autre possibilité, quelque peu moins souple à cause de son point d'intersection fixe à 0, est la courbe de puissance :

(11)

L = a X^{b}

où le taux absolu de croissance selon l'âge est décrit par :

(11)

g_{x} = a b X^{b}

La famille des courbes exponentielles et des courbes de puissance peut servir à ajuster pratiquement toute courbe de croissance présentant une croissance monotone et ne contenant pas de point d'inflexion. Ces courbes ne conviennent pas aux courbes de croissance en S, mais elles ont été utilisées très efficacement pour décrire de courts intervalles de croissance, en particulier aux stades larvaires (Beckman et Dean 1984; Gjosaeter 1987; Tzeng et Yu 1988; Campana et Hurley 1989). Le degré de courbure dépendant de la valeur de l'exposant, les courbes exponentielles et les courbes de puissance peuvent servir à ajuster des séquences en ligne droite et des courbes. C'est pourquoi elles sont considérées comme des descripteurs facilement ajustés, mais puissants, pour les courtes séquences de croissance (Ricker 1979). Des exemples de modèles exponentiels et de puissance sont présentés à la figure 4.

Exemples de modèles applicables à des courbes curvilignes sans point d'inflexion. (En haut) Le modèle exponentiel est souvent appliqué à de courtes séquences de croissance étant donné que le degré de courbure dépend de la valeur de l'exposant. (En bas) La courbure de la courbe de puissance ajustée (2,61 âge0,37) dépend aussi de la valeur de l'exposant, mais ce type de courbe passe par l'origine, ce qui la contraint. Au besoin, un paramètre d'intersection peut y être ajouté (p. ex., Y = point d'intersection + aXb) pour supprimer cette contrainte. Bien que la version du modèle de von Bertalanffy fondé sur la longueur [Y = 14,98 (1-exp (-0,0247 (X + 12,10)))] ne soit pas ainsi contraint à l'origine, il ne peut pas être appliqué à des données présentant une distribution sigmoïde, au contraire du type pondéré.

Le modèle de Gompertz, également dit modèle de Laird-Gompertz (Gompertz 1825; Laird et al. 1965), est aujourd'hui le modèle de croissance des jeunes poissons le plus souvent appliqué, en particulier dans le cas des larves (p. ex., Methot et Kramer 1979; Lough et al. 1982; Warlen et Chester 1985; McGurk 1987). Comme le modèle logistique et le modèle de von Bertalanffy, le modèle de Gompertz convient bien aux descriptions de la croissance sigmoïde (figure 5). Certains partisans de ce modèle ont proposé qu'il soit le premier choix pour modéliser la croissance des poissons (Zweifel et Lasker 1976). Toutefois, comme d'autres modèles, il peut rarement être utilisé pour décrire tous les stades du cycle biologique d'une espèce (Ricker 1979). Ricker (1979) présente trois autres formes de ce modèle, soit :

(13)

L = L_{0} exp [k (l - exp {- G X})]

(14)

L = L_{¥} exp [- k exp (- G X)]

(15)

L = L_{¥} exp [- exp (- G {X - X_{0}})]

où L₀ est la longueur à l'âge X = 0, L_¥ est la longueur asymptotique, G est le taux instantané de croissance à l'âge X₀, X₀ est le point d'inflexion de la courbe et l'âge auquel le taux de croissance absolu commence à diminuer et k est un paramètre adimensionnel. Le taux absolu de croissance (g) à l'âge X est obtenu comme suit :

(16)

g_{x} = G L_{x} (ln L_{¥} - ln L_{x})

Le modèle de croissance logistique donne souvent un ajustement de la courbe de croissance très semblable à celui du modèle de Gompertz (figure 5). Ils diffèrent cependant, car dans le premier, les parties au-dessus et en dessous du point d'inflexion sont symétriques contrairement à celles de la courbe de Gompertz. L'effet de cette différence est difficile à voir sauf lorsque les données s'étendent bien au-delà du point d'inflexion, de part et d'autre. La courbe logistique peut prendre les deux formes suivantes :

(17)

L = L_{¥} {(1 + exp [- G (X - X_{0})])}^{- l}

(18)

L = L_{¥} {(l + c exp [- G X])}^{- 1}

où G est le taux de croissance instantané à l'origine de la courbe, X₀ est l'âge au point d'inflexion de la courbe et l'âge auquel le taux absolu de croissance atteint son maximum, et c est le paramètre à estimer. Le taux absolu de croissance (g) de la courbe logistique à l'âge X est :

(19)

g_{x} = G L_{x} (L_{¥} - L_{x}) {(L_{¥})}^{- 1}

La courbe logistique, habituellement utilisée pour décrire l'accroissement de populations, constitue le fondement des modèles de production excédentaire dans le domaine halieutique. Elle a toutefois aussi été utilisée pour modéliser la croissance de poissons individuels (Nishimura et Yamada 1984; Campana et Hurley 1989).

Examples of the Gompertz, logistic, and von Bertalanffy (weight) growth models fit to a set of simulated sigmoidal length at age data.

Exemples des modèles de croissance de Gompertz, logistique et de von Bertalanffy appliqués à une série de données simulées sur la longueur selon l'âge en courbe sigmoïde. Les courbes ajustées sont : Longueur = 12,29 exp(-exp(-0,0459(X-39,70))) – Modèle de Gompertz; Longueur = 11,39/(1+exp(-0,0777(X-46,40))) – Modèle logistique; Longueur = 13,00(1-exp(-0,0353(X – 4,754)))³ – Modèle de von Bertalanffy.

Le modèle de croissance de von Bertalanffy (von Bertalanffy 1938) a longtemps été utilisé pour décrire la croissance de poissons adultes (Ricker 1979), mais il a aussi été appliqué aux premiers stades de leur cycle biologique (Ralston 1976; Wild et Foreman 1980; Laroche et al. 1982; Young et al. 1988). Le modèle fondé sur une longueur standard s'applique à la plupart des données sur la croissance sans point d'inflexion (figure 4b), mais il ne convient pas à un régime de croissance sigmoïde. Il prend la forme suivante :

(20)

L = L_{¥} (1 - exp [- K (X - X_{0})])

et le taux absolu de croissance selon l'âge est décrit par :

(21)

g_{x} = K (L_{¥} - L_{x})

où K est le coefficient de croissance de von Bertalanffy (ou de Brody ou de Putter) et X₀ est l'âge auquel la longueur d'un poisson est nulle, selon les calculs prédictifs. La prudence est de mise dans l'interprétation des paramètres de von Bertalanffy, car la terminologie peut induire en erreur. Le coefficient de croissance K est une mesure du taux auquel le taux de croissance diminue et non une mesure du taux de croissance en soi. Plus important encore pour les chercheurs étudiant la croissance de jeunes poissons, X₀ est un simple paramètre statistique; il correspond rarement à l'âge du poisson à l'éclosion. Comme dans le cas des autres modèles de croissance, le modèle de von Bertalanffy doit être choisi selon des critères de qualité de l'ajustement et de commodité. Toutefois, nous le considérons en général comme moins adapté pour la croissance des larves que d'autres modèles, principalement parce qu'il ne peut pas être appliqué à des données de croissance en courbe sigmoïde. On peut améliorer son caractère général en utilisant l'équation (20) du troisième degré, conçue pour modéliser la prise de poids, afin d'ajuster des données de longueur ou de poids montrant une inflexion de la croissance (figure 5) :

(22)

W = W_{¥} {(l - exp [- k (t - t_{0})])}^{3}

Modèles de croissance âge-température

Les modèles de croissance présentés ci-dessus sont considérés comme les meilleurs modèles de prédiction de la longueur et du taux de croissance lorsque seules des données sur l'âge sont disponibles. L'âge est évidemment une variable explicative utile de la taille d'un poisson. Toutefois, la nourriture et la température ont une forte incidence sur le taux de croissance des poissons (Brett 1979) et ces deux variables peuvent varier considérablement d'une population, d'une date d'échantillonnage et d'un milieu de vie à l'autre. Par conséquent, les modèles de croissance structurés par âge se révèlent parfois peu utiles dans les comparaisons entre taux de croissance de différents milieux.

À notre connaissance, il n'existe pas de modèle de croissance structuré par âge qui inclue les variables nourriture et température et puisse être facilement paramétré sur le terrain. Toutefois, lorsque des données sur la température sont disponibles, un modèle de croissance modulé par l'âge et la température peut se révéler précieux pour prédire le taux de croissance de jeunes poissons dans divers milieux (Campana et Hurley 1989). Ce modèle convient particulièrement lorsque l'écart dans les données de température est très prononcé ou bien lorsque la croissance de l'espèce en question est particulièrement sensible à de petits gradients de température. Ces conditions sont le plus souvent réunies lorsque plusieurs échantillons ont été prélevés dans un milieu hétérogène ou lorsque les échantillons ont été prélevés à différents moments de l'année.

Le modèle de croissance basé sur l'âge et la température se fonde sur le modèle logistique de croissance décrit ci-dessus (équation 17) [Campana et Hurley 1989]. Il a été clairement établi que la température a une incidence sur le taux de croissance absolu des poissons, qui diminue au-delà d'une température optimale (Brett 1979; Ricker 1979). Le taux de croissance absolu variant avec l'âge dans le modèle logistique, le modèle âge-température intègre un terme parabolique de température qui sert à modifier quotidiennement le taux de croissance absolu. Le modèle prend la forme générale suivante :

(23)

L_{âge} = L_{éclosion} + \sum_{t = 0}^{age} (taux de croissance absolu ⨯ terme de la température) dt

En utilisant l'équation (19) pour obtenir le taux de croissance absolu de la courbe logistique et l'équation décrivant une parabole pour la température, et en supposant que le modèle est ajusté tous les jours, on obtient :

(24)

L_{age} = L_{hatch} + K ⨯ \sum_{t = 0}^{age} (G l_{t} - G {l_{t}^{2} L_{\infty}}^{-1}) ⨯ (c - {(T_{t} - T_{opt})}^{2})

où l_t = L_¥(l + exp[-G(t - t₀)])-1; G, L_¥, t₀, c, and T_opt (= température optimale) sont les paramètres du modèle et Lhatch et K sont des paramètres fixes à déterminer indépendamment. Au premier abord, l'équation (24) a l'air intimidante. Pourtant, elle nécessite peu de données, celles-ci se limitant aux âges et aux températures quotidiennes auxquelles chaque larve a été exposée. Une fois les données préparées, le modèle peut être ajusté à l'aide d'une des méthodes de régression non linéaire. Est présenté à la figure 6 un exemple de ce modèle ajusté tiré d'une étude de Campana et Hurley (1989). Les données proviennent de cinq campagnes d'échantillonnage indépendantes, effectuées à un mois d'intervalle.

FIGURE 6. Le modèle de croissance âge-température associe une équation de croissance logistique à un terme parabolique de température, qui modifie quotidiennement le taux de croissance absolu. Dans cet exemple tiré d'une étude de Campana et Hurley (1989), l'équation prend la forme de l'équation 24, où G = 0,0502, L_¥ = 59,18, t₀ = 60,57, c = 22,77, T_opt = 5,925, L_hatch = 3,0 et K = 0,2. Les longueurs ont subi une transformation logarithmique (ln) afin de stabiliser la variance. La ligne ajustée semble irrégulière parce que seule une des deux variables indépendantes est illustrée.

Deux points doivent être clarifiés. En premier lieu, le modèle âge-température peut et devrait être ajusté à l'aide d'échantillons groupés (plutôt que d'un échantillon à la fois). Étant donné que le modèle a été conçu pour analyser les effets de la température sur la croissance, le regroupement des échantillons expose davantage les différences entre les données, ce qui améliore le niveau de discrimination de ces effets dans le modèle. En deuxième lieu, toute analyse requiert l'examen des résidus de modèle (voir ci-dessous), mais cela est particulièrement important dans le cas de ce modèle-ci. Le modèle est considéré comme satisfaisant seulement si les résidus des valeurs prédites, des tailles, des âges et des températures sont distribués au hasard, pour les échantillons d'une même campagne et entre campagnes.

Puisque le modèle âge-température inclut l'effet de la température sur le taux de croissance pour chaque jour de la vie d'un jeune poisson, une série de températures quotidiennes, plutôt qu'une estimation ponctuelle, est requise pour chaque poisson. Normalement, on considère que tous les poissons d'un échantillon donné ont été exposés à la même température à une date donnée. Toutefois, les données de température quotidienne ne sont pas toujours disponibles pour chaque échantillon. On peut obtenir une approximation valable de la série de températures quotidiennes en ajustant une courbe à des mesures périodiques (p. ex., mensuelles). Campana et Hurley (1989) donnent un exemple de cette méthode. Ils ont ajusté une courbe sinusoïdale à chaque température moyenne mensuelle, puis ont utilisé l'équation obtenue pour estimer la température de chaque jour.

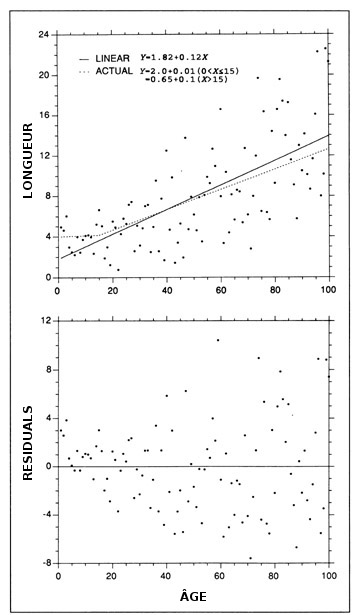
Erreurs communes d'ajustement des modèles

Dans tout modèle ajusté, on doit s'assurer que les résidus sont distribués au hasard et que la variance est constante pour l'ensemble des données. Si on n'étudie pas ces deux dernières hypothèses, les estimations du taux de croissance peuvent être inexactes, biaisées à certains âges ou excessivement influencées par des valeurs aberrantes. Dans l'exemple de la figure 7, la régression linéaire ajustée semble bien représenter la plupart des données simulées. Mais les résidus aux jeunes âges ne sont pas distribués au hasard, ce qui indique que le modèle ne devrait pas être appliqué aux données sur les jeunes poissons. Les calculs du taux de croissance reposant sur toute la série de données donneraient une surestimation du taux de croissance des jeunes poissons (< 15 j) de plus d'un ordre de grandeur. Un effet semblable peut être produit par l'inclusion de données à effet multiplicateur élevé, permettant de forcer une régression à passer à travers ou près de points de données isolés à des valeurs de X très élevées (ou très basses) aux dépens de la qualité de l'ajustement des autres données. Cet effet doit se manifester comme une tendance des résidus ou, de manière équivalente, un changement marqué des paramètres de régression après la suppression des données à effet multiplicateur élevé. L'influence d'une variance accrue avec l'âge (hétéroscédasticité) [figure 7] se reflète par une influence exagérée, sur la pente de la droite de régression des données portant sur les poissons âgés. Le retrait d'une valeur aberrante pour les poissons âgés a causé un changement de pente deux fois plus marqué que celui produit par le retrait d'une valeur aberrante proportionnellement équivalente pour les jeunes poissons. Pour obtenir une estimation robuste et précise du taux de croissance des poissons à la figure 7, il faudrait ajuster une régression linéaire seulement aux données correspondant aux poissons de plus de 15 j, après les avoir transformées pour stabiliser la variance.

Exemple d'erreurs communes commises dans l'ajustement de modèle de croissance. (En haut) La relation sous-jacente réelle est un processus linéaire à deux échelons où la pente (taux de croissance) augmente d'un facteur 10 après l'âge de 15 j (ligne pointillée). Un terme d'erreur distribué normalement et proportionnel à la moyenne a été ajouté à la relation sous-jacente. À première vue, une régression linéaire (ligne pleine) semble bien représenter les données. (En bas) L'examen des résidus indique que l'ajustement d'une seule régression linéaire aux données ne convient pas; les résidus ne sont pas distribués au hasard par rapport à la régression, en particulier aux jeunes âges, et la variance augmente selon l'âge (hétéroscédastique), ce qui accroît l'influence des observations individuelles concernant les poissons âgés par rapport à celles portant sur les jeunes poissons. L'utilisation de la régression ajustée pour estimer le taux de croissance surestimerait le taux de croissance des jeunes poissons d'un facteur 12.

Rétrocalcul de la croissance

Les rétrocalculs de croissance fondés sur une série d'accroissements journaliers sont très certainement l'application la plus efficace de l'examen des microstructures d'otolithes. En théorie, il est possible d'utiliser les largeurs d'une série chronologique d'accroissements journaliers, avec une relation longueur des poissons-taille des otolithes, pour déterminer la longueur et le taux de croissance d'un poisson pour chaque jour de son cycle biologique. En pratique, de tels calculs souffrent d'un certain nombre de contraintes logistiques et théoriques (Campana et Neilson 1985; Bradford et Geen 1987; Secor et Dean, 1989; Neilson, dans la publication citée en haut de la page), qui devront toutes être réglées avant d'utiliser les méthodes de rétrocalcul présentées ci-après.

Problèmes des rétrocalculs classiques de la croissance

Pratiquement toutes les méthodes de rétrocalcul de la croissance reposent sur l'hypothèse d'une proportionnalité (soit une relation linéaire) entre la taille des otolithes (ou des écailles ou d'une structure osseuse) et la longueur des poissons (Carlander 1981; Bartlett et al. 1984; Weisberg 1986; Smale et Taylor 1987; Campana 1990). Que les rétrocalculs soient fondés sur le nombre d' annuli ou d'accroissements journaliers, deux hypothèses sous-jacentes s'appliquent : (a) la marque périodique (p. ex., accroissement journalier) est formée à intervalles constants et (b) la distance entre les marques consécutives est proportionnelle à la croissance du poisson. La validation de la fréquence de formation des accroissements, traitée en détail dans la publication citée en haut de la page (Geffen), est une étape essentielle de l'examen des microstructures d'otolithes. Bien qu'il soit préférable d'avoir une séquence complète validée d'accroissements journaliers, il est possible de réaliser des rétrocalculs y compris si le début de la croissance d'un otolithe semble caractérisé par la formation d'accroissements non journaliers (p. ex., chez le hareng [Campana et al. 1987]). Dans ces cas, les rétrocalculs ne portent que sur la région contiguë entre la date d'échantillonnage (bord de l'otolithe) et le début de la série continue d'accroissements journaliers. Bien entendu, ces calculs doivent être présentés comme une fonction de la taille à une date plutôt qu'à un âge donné. Quant à l'hypothèse de proportionnalité entre la croissance d'un poisson et celle de son otolithe, elle a en général été justifiée par des corrélations empiriques entre les variables de taille du poisson et de taille de l'otolithe. Ces corrélations et diverses études expérimentales (Wilson et Larkin 1982; Volk et al. 1984) indiquent certainement une correspondance générale entre ces variables, mais cette dernière ne s'applique pas nécessairement à un niveau individuel ou détaillé, comme cela a été montré (Gutiérrez et Morales-Nin 1986; Bradford et Geen 1987). Dans une certaine mesure, la rupture apparente entre la croissance d'un poisson et de ses otolithes est fonction d'une corrélation récemment établie entre le taux de croissance et la relation poisson-otolithe (Mosegaard et al. 1988; Reznick et al. 1989; Secor et Dean 1989). Il existe toutefois un certain nombre d'espèces pour lesquelles la relation entre la longueur des individus et la taille de leurs otolithes est fondamentalement non linéaire. Il est donc difficile de rétrocalculer leur croissance à moins de pouvoir décrire la relation mathématiquement (p. ex., Butler 1989). Lorsque le rétrocalcul est réalisé à partir d'une relation poisson-otolithe curvilinéaire, l'hypothèse implicite veut que le point d'inflexion de la courbe se produise à la même taille poisson-otolithe pour chaque poisson. Dans la plupart des cas, il est peu probable que cette hypothèse se vérifie, mais on ne sait pas encore quelles en sont les répercussions.

Il est conseillé d'utiliser avec prudence la régression et la méthode de Fraser-Lee classiques (Carlander 1981), ou de ne pas les utiliser, car elles sont susceptibles d'introduire un biais dans les rétrocalculs reposant sur la microstructure des otolithes (Campana 1990). Comme dans la plupart des méthodes de rétrocalcul, elles supposent une relation linéaire entre la longueur d'un poisson et la taille de ses otolithes. La régression estime la longueur d'un poisson (L) à un âge précédent (a) par inclusion de la taille de ses otolithes (O) à l'âge a dans une équation de régression de la longueur par rapport à la taille, dérivée d'échantillons de la population, comme suit :

(25)

L_{a} = b o_{a} + d

où b et d sont respectivement la pente et le point d'intersection de la régression. Parce que cette méthode suppose que les mesures de chaque poisson et otolithe ne dévient pas de la régression globale, elle est généralement utilisée pour s'intéresser aux longueurs moyennes rétrocalculées plutôt qu'aux valeurs individuelles. En revanche, la méthode de Fraser-Lee (ou de Lee) suppose que toute déviation d'une mesure individuelle par rapport à la régression poisson-otolithe totale soit observée proportionnellement aux longueurs rétrocalculées, comme suit :

(25)

L_{a} = d + (L_{c} - d) O_{c}^{-1} O_{a}

où L_c et Oc sont respectivement la longueur du poisson et la taille de ses otolithes au moment de la capture. Alors que la méthode de Fraser-Lee n'intègre pas directement la pente de la droite de régression, il est évident que la pente a un effet sur la valeur du point d'intersection de cette dernière. La seule différence sur le plan algébrique entre la régression et la méthode de Fraser-Lee, c'est que le point d'intersection de cette dernière est corrigé. Par conséquent, les deux méthodes donnent des longueurs moyennes rétrocalculées identiques, bien que les valeurs rétrocalculées pour chaque individu puissent différer (figure 8). La régression et la méthode de Fraser-Lee étant sensibles à la valeur de point d'intersection utilisée, des modèles linéaires et de vraisemblance maximale plus perfectionnés ont été conçus afin de tenir compte des variations dépendant de l'âge et des échantillons dans la relation poisson-otolithe (Bartlett et al. 1984; Weisberg 1986; Smith 1987). Toutefois, toutes les méthodes supposent que cette relation ne varie pas systématiquement en fonction du taux de croissance et, en outre, que l'un des paramètres de régression, ou les deux, peuvent être précisément estimés à partir de la population. Il a maintenant été prouvé sans équivoque que cette relation varie systématiquement en fonction du taux de croissance des poissons : chez les poissons à croissance lente, les otolithes sont plus volumineux et plus lourds que ceux des poissons à croissance rapide de même taille (Templeman et Squires 1956; Boehlert 1985; Mosegaard et al. 1988; Reznick et al. 1989; Secor et Dean 1989). En outre, une étude récente a révélé que les variations individuelles du taux de croissance produisent une régression poisson-otolithe à l'échelle de la population qui diffère significativement de la moyenne pour un poisson individuel (Campana 1990). Il en résulte finalement que les rétrocalculs de croissance classiques sont susceptibles de sous-estimer les longueurs selon l'âge précédentes, une conclusion qui semble expliquer l'ubiquité apparente du phénomène de Lee.

Exemple de rétrocalculs de croissance de poissons individuels d'après une analyse de régression (R), la méthode de Fraser-Lee (FL) et la méthode du point d'intersection biologique (B). Les rétrocalculs reposant sur une analyse de régression supposent qu'il n'existe aucun écart de la régression globale, tandis que ceux faisant appel à la méthode de Fraser-Lee supposent que les écarts poisson-otolithe restent proportionnels tout au long du rétrocalcul. Les deux méthodes donnent des longueurs moyennes rétrocalculées égales à la régression ajustée globale (ligne pleine). À l'inverse, la méthode du point d'intersection biologique (équation 27) n'est en aucune manière sous l'effet de la régression ajustée globale; la pente de chaque droite poisson-otolithe est indépendante de toutes les autres de l'échantillon. Dans cet exemple, des observations indépendantes auraient permis d'établir que la croissance du poisson et de ses otolithes était proportionnelle après le point d'intersection biologique qui, dans cet exemple, s'est produit lorsque l'otolithe mesurait 2,0 et le poisson 1,0.

Rétrocalculs reposant sur l'algorithme du point d'intersection biologique

L'algorithme de rétrocalcul du point d'intersection biologique est une version modifiée de l'équation de Fraser-Lee faisant appel à une valeur du point d'intersection établie d'après des paramètres biologiques plutôt que statistiques (Campana 1990). À l'instar de la méthode de Fraser-Lee, la méthode du point d'intersection biologique suppose une proportionnalité de la croissance d'un poisson et celle de ses otolithes. Toutefois, contrairement à la première méthode, elle détermine la valeur du point d'intersection par la taille moyenne du poisson et de son otolithe au début de la proportionnalité et elle n'est donc pas sensible aux variations des paramètres de régression entre échantillons. En effet, les seuls échantillons nécessaires à la méthode du point d'intersection biologique sont ceux servant à vérifier la proportionnalité de la croissance des poissons et des otolithes après ce point. Dans de nombreux cas, on l'établit simplement en mesurant la longueur de larves nouvellement écloses et la taille de leurs otolithes en laboratoire. Cette méthode est aussi insensible à l'effet du taux de croissance décrit ci-dessus, étant donné que la pente poisson-otolithe est calculée indépendamment pour chaque poisson. En dernier lieu, la précision des rétrocalculs est relativement insensible à la variation normale entourant la valeur du point d'intersection, en grande partie à cause des petites valeurs impliquées. L'équation est la suivante :

(27)

L_{a} = L_{c} + (O - O_{c}) (L_{c} - L_{i}) {(O_{c} - O_{i})}^{-1}

où L_i et O_i sont respectivement la longueur du poisson et la taille de ses otolithes au point d'interception biologique. Un exemple de rétrocalcul est présenté à la figure 8. Il convient de noter que la pente et le point d'intersection pour les poissons échantillonnés ne sont pas utilisés dans les rétrocalculs. Si une étude indépendante a permis de déterminer que la croissance des poissons et de leurs otolithes est proportionnelle depuis l'éclosion, il peut être justifié de rétrocalculer la croissance depuis ce moment. À l'inverse, les rétrocalculs fondés sur la régression ou la méthode de Fraser-Lee ne doivent porter que sur la fourchette des longueurs des poissons échantillonnés et des tailles de leurs otolithes.

Dans certains cas, les différences entre les rétrocalculs de croissance réalisés à l'aide de méthodes classiques et ceux reposant sur la méthode du point d'intersection biologique sont relativement faibles. On le constate particulièrement lorsque les points d'intersection statistique et biologique sont colinéaires, notamment en cas de prélèvement d'échantillons de très jeunes poissons (d'une taille s'approchant du point d'intersection biologique). Toutefois, la méthode du point d'intersection biologique est toujours au moins aussi précise, sinon plus, que les méthodes classiques. Il faut néanmoins bien comprendre que toutes les méthodes susmentionnées reposent sur l'hypothèse d'une relation linéaire constante entre la longueur des poissons et la taille de leurs otolithes. Ni les méthodes classiques ni la méthode du point d'intersection biologique ne donnent des valeurs rétrocalculées exactes si les relations poisson-otolithe ne sont pas linéaires (Campana 1990; Secor et Dean 1992).

Rétrocalculs reposant sur des algorithmes multivariés

Lorsqu'il existe une relation intrinsèquement curvilinéaire entre la longueur des poissons et la taille de leurs otolithes, la transformation des données en forme linéaire permet d'utiliser l'équation (27). Toutefois, lorsque les taux de croissance varient dans le temps, les méthodes linéaires de rétrocalcul décrites dans la section précédente donnent des résultats en partie erronés. De plus en plus d'éléments tendent à montrer que la largeur d'un accroissement journalier est liée plus étroitement à la vitesse du métabolisme et/ou à la température qu'à la croissance somatique (Mosegaard et al. 1988; Wright 1991; Secor et Dean 1992). Si cela se confirme, toute méthode fiable de rétrocalcul de la croissance devra presque certainement inclure une chronologie de la vitesse de métabolisme ou de la température. Cette méthode n'a toutefois pas encore été conçue. Il existe toutefois deux algorithmes multivariés, tous deux très expérimentaux, qui utilisent des indicateurs pour le terme vitesse de métabolisme/température. Secor et Dean (1989, 1992) soutiennent que l'âge a une incidence cumulative sur la relation entre la taille des otolithes et la longueur des poissons, qui engendre des otolithes de tailles différentes chez les poissons à croissance lente et ceux à croissance rapide de même longueur. Les rétrocalculs de la croissance reposant sur leur modèle ont permis de déterminer avec précision l'évolution de la croissance de poissons élevés en laboratoire, mais ont donné des résultats médiocres pour les poissons élevés en étang (Secor et Dean 1992). À partir d'un raisonnement différent, Campana (1990) a suggéré que les longueurs précédentes selon l'âge pourraient être estimées d'après une série de largeurs d'accroissements journaliers et d'une estimation de l'ampleur de l'effet du taux de croissance sur la relation poisson-otolithe. Il a présenté un algorithme qui n'a pas été étudié. Pour l'heure, il n'existe donc pas d'algorithme de rétrocalcul susceptible d'estimer précisément la croissance passée dans toutes les conditions. En outre, aucune des méthodes de rétrocalcul proposées ne tient compte du fait que la croissance des otolithes a tendance à être lisse par rapport à la croissance du poisson (Campana et Neilson 1985). Il faut recourir à des modèles en série chronologique lorsqu'on doit tenir compte de largeurs d'accroissements autocorrélées (Gutiérrez et Morales-Nin 1986). De fait, ils semblent bien se prêter à l'analyse de ce genre de données.

Rétrocalcul de la croissance récente

Soit une proportionnalité exacte de la croissance d'un poisson et de ses otolithes, la largeur des accroissements journaliers les plus récents devrait donner une mesure du taux de croissance récent. Il est difficile d'obtenir ces mesures par d'autres moyens, ce qui explique le grand intérêt qu'y portent les chercheurs étudiant les conditions environnementales propices à la survie des jeunes poissons (Methot 1981; Thomas 1986; Bailey 1989; Suthers et al. 1989; Powell et al. 1990; Hovenkamp et Witte 1991). Les hypothèses sous-tendant l'utilisation des largeurs des accroissements comme indicateurs du taux de croissance instantané sont les mêmes que celles présentées ci-dessus pour les rétrocalculs de croissance en général. Toutefois, l'échelle de l'analyse rend les inférences obtenues considérablement plus sensibles à des déviations par rapport aux hypothèses. En particulier, les déviations à court terme par rapport à une relation linéaire poisson-otolithe sont plus visibles quotidiennement que si l'on réalise une moyenne pour tout le cycle biologique. C'est pourquoi la plupart des chercheurs ont utilisé des groupes d'accroissements, comprenant par exemple ceux correspondant aux 7 à 30 derniers jours de vie, comme indice du taux de croissance récent. L'utilisation de largeurs d'accroissements groupées réduit, mais ne supprime pas, l'effet de la croissance autocorrélée des otolithes et de la curvilinéarité sur une courte période de la relation poisson-otolithe. Il reste qu'à notre connaissance, aucune étude n'a évalué le niveau de regroupement requis.

L'estimation des taux de croissance récents fondée sur la croissance des otolithes comporte trois étapes fondamentales : la mesure de la largeur des accroissements, l'établissement d'une relation poisson-otolithe quantitative (généralement linéaire, mais pas nécessairement) et la conversion du taux de croissance des otolithes en taux de croissance des poissons. La mesure des derniers accroissements journaliers le long d'un radius préétabli, isolément ou ensemble, a déjà été discutée (Campana, dans la publication citée en haut de la page). La relation poisson-otolithe peut être établie par simple régression de la longueur des poissons par rapport à la taille des otolithes, si la croissance des deux est proportionnelle. Dans ce cas, les résidus de la régression sont distribués au hasard de part et d'autre de zéro pour ce qui est de la taille des otolithes. Soulignons qu'il est préférable de considérer la longueur du poisson comme la variable dépendante, étant donné que cette longueur (plutôt que la taille des otolithes) est la variable à prédire. Quand la taille des otolithes augmente curvilinéairement par rapport à la longueur du poisson, la transformation logarithmique des mesures des otolithes suffit souvent à produire la linéarité, quoiqu'il faille le vérifier. On ne peut trop insister sur l'importance de l'obtention d'une relation poisson-otolithe linéaire, étant donné que la largeur des accroissements peut augmenter en fonction de la taille des otolithes, y compris lorsque le taux de croissance du poisson est constant (ou à la baisse dans certains cas), si la relation poisson-otolithe n'est pas linéaire. Enfin, les tailles des otolithes (transformées) sont converties en longueurs de poissons à l'aide de l'équation 27, puis interprétées en matière de taux de croissance quotidiens après division du changement net de longueur du poisson par le nombre d'accroissements journaliers compris dans le groupe mesuré. Comme l'équation 27 renferme un ajustement inhérent des variations individuelles de la taille des otolithes chez les poissons de même longueur, la correction de taille utilisée par Methot (1981) est inutile ici.

Le rétrocalcul des patrons de croissance récents souffre des mêmes contraintes que celles décrites dans les deux dernières sections. Plus particulièrement, la non-linéarité de la relation poisson-otolithe imputable à la croissance, la vitesse de métabolisme et/ou la température introduisent des erreurs dans les rétrocalculs qui en découlent. En effet, ces erreurs peuvent être davantage marquées lorsqu'on rétrocalcule le taux de croissance récent que lorsqu'on estime le taux de croissance à un stade moins avancé du cycle biologique à cause de l'incidence importante d'un changement récent de la pente de la relation poisson-otolithe basée sur les longueurs rétrocalculées. Aucune méthode n'a encore été publiée pour régler cette difficulté. On peut toutefois l'éviter en démontrant que la pente de la relation poisson-otolithe reliant des échantillons prélevés juste avant et juste après la période de croissance en question est semblable à la pente utilisée pour les rétrocalculs.

Croissance et environnement

Les analyses conçues en vue d'établir un lien entre la chronologie de la croissance mise en évidence dans l'otolithe et les observations sur l'environnement connexes constituent l'une des applications les plus prometteuses et les plus complexes de l'examen des microstructures d'otolithes. En théorie, ces analyses pourraient servir à étudier de nombreuses hypothèses actuelles relatives à la croissance, à la survie et au recrutement. Toutefois, un test probant d'une relation environnement-croissance est loin d'être simple : une simple corrélation ou régression d'un indice de croissance par rapport à une ou plusieurs variables environnementales peut gravement induire en erreur. Des méthodes statistiques valides d'analyse de données sur les otolithes et l'environnement sont encore en cours d'élaboration. En la matière, le domaine parallèle de la dendrochronologie (datation par les anneaux de croissance des arbres) est beaucoup plus développé que le nôtre. Nous recommandons aux chercheurs souhaitant réaliser des analyses otolithe-environnement de consulter les ouvrages sur la datation par les cernes des arbres et de prendre note du fait qu'ils se fondent sur l'analyse de séries chronologiques et des modèles linéaires généraux (Fritts 1976; Hughes et al. 1984; Stahle et al. 1988).

Les indices de croissance permettant une analyse par rapport à des variables environnementales peuvent être classés en trois grandes catégories de séries chronologiques : taux de croissance récent, taux de croissance moyen et taux de croissance individuel. Tous sont des indices valides de la croissance, mais les moyens de les interpréter varient considérablement. Ainsi, on a souvent établi une relation entre des indices de croissance récents et des variables environnementales (p. ex., Methot 1981; Thomas 1986; Bailey 1989; Karakiri et al. 1989; Suthers et al. 1989; Hovenkamp et Witte 1991), dans un sens relatif ou par corrélation (p. ex., la température et la croissance récente rétrocalculée, comme l'indique la largeur moyenne des accroissements formés dans les 10 derniers jours, qui est plus élevée sur le site A que sur le site B). L'avantage de cette approche vient de l'indépendance des observations : chaque poisson donne une estimation unique du taux de croissance récent, ce qui élimine les problèmes statistiques de croissance autocorrélée des otolithes. Cependant, le danger présenté par cette méthode apparaît clairement si l'analyse n'étudie pas explicitement la possibilité d'un taux de croissance plus rapide chez les gros individus. Vu que ces derniers connaissent souvent des taux de croissance absolus plus élevés que les petits poissons et étant donné les différences de taille moyenne entre échantillons, les différences entre indices de croissance récents des différents échantillons peuvent fort bien être causées par des différences de tailles entre échantillons et être attribuées à tort à des variables environnementales. Suthers et al. (1989) ont utilisé une simple analyse de la covariance pour surmonter ce problème lorsqu'ils ont tenté d'établir une corrélation entre les facteurs environnementaux et l'augmentation du taux de croissance de la morue (Gadus morhua).

Une deuxième méthode consiste à établir une relation entre le taux de croissance moyen, plutôt que le taux de croissance récent, et une combinaison de variables environnementales. Cette approche est recommandée seulement pour des poissons très jeunes, ne serait-ce que parce que les fluctuations environnementales pendant une période prolongée peuvent brouiller l'interprétation des données de croissance correspondantes. Plusieurs chercheurs ont réussi à établir une relation entre, d'une part, les taux de croissance de jeunes larves appartenant à des cohortes spécifiques et, d'autre part, la température et d'autres variables (Methot et Kramer 1979; Crecco et Savoy 1985).

Bien que l'analyse de la séquence entière des largeurs des accroissements journaliers de chaque otolithe puisse être l'indice de croissance le plus efficace, l'autocorrélation inhérente de la croissance des otolithes vient la compliquer. Il en résulte que les taux de croissance rétrocalculés ne sont pas indépendants; il est donc difficile d'établir une relation statistique entre eux et une autre série chronologique de variables. Ce problème peut expliquer les résultats inattendus obtenus par certains chercheurs lorsqu'ils ont fait une régression de séries chronologiques de variables environnementales par rapport à des séquences de taux de croissance rétrocalculés (p. ex., Barkman et Bengtson 1987). D'une manière novatrice et statistiquement rigoureuse, Thorrold et Williams (1989) ont effectué une analyse de variance à mesures répétées, suivie d'un contraste polynomial en fonction du temps, afin d'établir s'il existait des différences de séquences d'accroissements entre cohortes. Ils ont ensuite interprété les différences observées qualitativement par rapport aux variables environnementales. Cependant, l'analyse de séries chronologiques est la méthode la plus efficace et la plus souvent utilisée par les dendrochronologistes. L'analyse des séries, en particulier de longues séquences de marques de croissance, exploite pleinement l'information disponible, tient explicitement compte de toute autocorrélation inhérente et se prête bien à la mise à l'épreuve d'une large gamme d'hypothèses relatives aux effets de l'environnement sur la croissance. Bien qu'elle convienne pour déceler les cycles dans les données sur la croissance (p. ex., cycles lunaires; Campana 1984), ses applications les plus puissantes ont permis de déterminer l'effet de variables environnementales sur la croissance (p. ex., Gutiérrez et Morales-Nin 1986; Thorrold et Williams 1989).

La corrélation illusoire est un problème sous-estimé susceptible de se présenter lorsqu'on tente d'établir une relation entre la croissance et des variables environnementales. La plupart du temps, elle se produit lorsque deux variables, chacune caractérisée par une tendance dans le temps, sont corrélées ou mises en relation par régression. Une tendance à la baisse dans des séries chronologiques de largeurs d'accroissements journaliers et de températures en est un exemple. Les deux séries peuvent être fortement corrélées, sans que cela soit dû à une relation inhérente entre elles, mais plutôt en grande partie aux tendances coïncidentes. Par exemple, la largeur à la baisse des accroissements peut être imputable uniquement aux taux de croissance réduits caractéristiques des poissons âgés. Étant donné que l'analyse de régression suppose que les observations sont indépendantes les unes des autres et que les observations tendancielles ne sont pas indépendantes, il faudrait, pour une analyse de régression plus appropriée, d'abord éliminer la tendance temporelle dans les deux séries chronologiques à l'aide des techniques disponibles (p. ex., calcul des différences premières; voir la documentation sur les séries chronologiques pour un complément d'information). Il faut en outre noter qu'une corrélation illusoire peut autant masquer les relations sous-jacentes qu'amplifier des relations inexistantes. Il faut absolument éliminer la tendance temporelle avant toute analyse de séries chronologiques, mais aussi avant de calculer la régression d'une série de variables environnementales par rapport à une séquence d'accroissements. Un sous-produit malheureux de l'élimination de la tendance temporelle est qu'elle peut supprimer à la fois les corrélations réelle et illusoire et donc rendre la méthode moins efficace. Thompson et Page (1989) présentent un bon exemple d'élimination de la tendance temporelle dans leur analyse séquentielle environnement-recrutement.

Analyse des dates d'éclosion

L'analyse des dates d'éclosion est l'un des outils les plus prometteurs de l'étude des processus de recrutement. Elle repose sur un principe simple : il est possible de calculer la distribution de la fréquence des dates d'éclosion des poissons survivants d'une population représentée par un échantillon aléatoire d'individus capturés à une date connue, dont l'âge a été déterminé par examen de la microstructure de leurs otolithes. Évidemment, la distribution des dates d'éclosion ainsi obtenue est une image transposée (image miroir) de la distribution des fréquences d'âges. On peut ensuite comparer la distribution des dates d'éclosion aux dates d'apparition observées de larves nouvellement écloses (ou d'œufs prêts à éclore). En l'absence de mortalité sélective, les formes de la distribution rétrocalculée des dates d'éclosion et de la distribution observée des dates d'apparition de larves devraient être identiques. Des différences entre les deux distributions (figure 9) donneraient toutefois à penser que le taux de survie des larves nées à certaines dates était plus élevé que celui de larves nées à d'autres dates. Il resterait donc à déterminer les facteurs environnementaux susceptibles d'agir sur le taux de survie relatif des cohortes quotidiennes et donc sur le succès du recrutement.

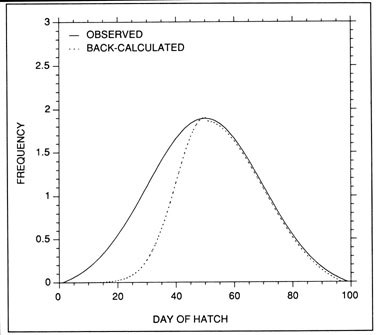
L'analyse des dates d'éclosion vise à établir une relation entre la distribution observée de la fréquence des dates d'éclosion (ou de la production d'œufs ou de larves) et celle des survivants. En principe, les différences entre les distributions observées et les distributions rétrocalculées indiquent que le taux de survie des larves écloses à certaines dates est plus élevé que celui de larves écloses à d'autres. Dans cet exemple, les larves écloses pendant la première moitié de la période de ponte montrent un taux de survie faible par rapport à celles écloses plus tard.

L'une des particularités les plus utiles de l'analyse des dates d'éclosion, c'est qu'elle met l'accent sur les caractéristiques des survivants plutôt que sur la population dans son ensemble. Les sources potentielles de mortalité chez les jeunes poissons sont nombreuses, mais seules certaines ont une incidence forte sur les effectifs des classes d'âge. Toutefois, lorsque certaines cohortes quotidiennes contribuent de manière disproportionnée à l'abondance des survivants, on peut être certain que des facteurs critiques agissant sur le recrutement sont entrés en jeu. Dans son étude d'avant-garde des dates d'éclosion, Methot (1983) a établi un rapport entre les différences mensuelles du taux relatif de survie des larves et divers signaux environnementaux, ainsi que l'effet global sur les effectifs des classes d'âge. Des études semblables sont en cours dans plusieurs pays, ce qui indique la valeur attribuée à ce type de recherche. Indubitablement, l'analyse des dates d'éclosion est une application potentiellement puissante de l'examen de la microstructure des otolithes. Elle ne doit cependant pas être considérée comme la panacée. Pour certains stades du cycle biologique et certaines espèces, l'analyse des dates d'éclosion servira tout juste à la description générale de ces dates. En effet, si on n'y prend pas garde, l'analyse des dates d'éclosion peut être plus trompeuse que révélatrice. La sélectivité des engins et la difficulté d'échantillonner adéquatement chaque stade pertinent du cycle biologique compliquent davantage la question (voir Butler, dans la publication citée en haut de la page). Dans la suite de la section sont présentées certaines propriétés et mises en garde associées à l'analyse des dates d'éclosion et quelques recommandations sur son utilisation.

Le problème le plus épineux des distributions de dates d'éclosion concerne leur instabilité. Alors que les dates de production des larves nouvellement écloses seraient normalement établies par un échantillonnage fréquent pendant toute la période d'éclosion des œufs, les distributions rétrocalculées des dates d'éclosion sont normalement établies d'après des échantillons prélevés pendant une période beaucoup plus courte. À cause de la mortalité naturelle, les larves écloses au tout début de la saison connaissent inévitablement un taux de mortalité cumulatif plus élevé que celles écloses plus tard. Par conséquent, les premières sont sous-représentées dans la distribution rétrocalculée des dates d'éclosion des œufs par rapport aux dernières. La distribution des dates d'éclosion est alors asymétrique et ne représente pas le nombre réel de survivants à un âge donné. Prenons l'exemple de la figure 10. Dans ce cas simple, on a simulé la distribution des dates d'éclosion d'un échantillon de post-larves en supposant que le taux instantané de mortalité constant après l'éclosion des œufs était de 0,1 j^-1. La période d'éclosion s'est étalée sur 30 j et les échantillons ont été prélevés 50 j après la fin de la période. La distribution rétrocalculée des dates d'éclosion est clairement asymétrique par rapport à la distribution initiale. Pourtant, à un âge donné (et non à une date donnée), les survivants de chaque cohorte quotidienne constituent la même proportion de la production initiale que toutes les autres cohortes quotidiennes. L'asymétrie de la distribution est uniquement due à la mortalité cumulée différentielle entre les larves les plus jeunes et les plus âgées. Dans cet exemple, les larves les plus âgées ont connu 30 j de mortalité de plus à une date donnée que les larves les plus jeunes, ce qui a donné lieu à une abondance des premières n'atteignant que 5 % de celle des larves les plus jeunes à une date donnée. Cette conclusion est valable indépendamment du taux de mortalité, de la durée de la période d'éclosion et de l'intervalle avant l'échantillonnage supposés. Dans tous les cas, la mortalité cumulée différentielle entre les larves les plus jeunes et les plus âgées commandera la forme de la distribution des dates d'éclosion. Ce phénomène est plus visible si on suppose que le taux de mortalité dans l'exemple ci-dessus chute à zéro à un âge donné. Dès que toutes les cohortes quotidiennes ont atteint cet âge, la mortalité cumulée différentielle entre les plus jeunes et les plus âgées est réduite à zéro, de sorte que la distribution rétrocalculée des dates d'éclosion devient identique à celle de la production initiale. Autrement dit, si les dates d'éclosion sont établies à partir d'un stade du cycle biologique connaissant un faible taux de mortalité, la distribution des dates d'éclosion qui en découle est relativement stable.

Exemple d'une distribution asymétrique de dates d'éclosion due uniquement à des différences dans le taux cumulé de mortalité entre les membres de la cohorte. On a supposé que la production de larves s'est prolongée symétriquement sur une période de 30 j (fréquences observées). Toutes les larves ont connu un taux de mortalité instantané de 0,1 j^-1. Bien que toutes les cohortes quotidiennes aient survécu également jusqu'à un âge donné, le taux de mortalité était suffisamment élevé pour que les premières larves écloses soient moins abondantes dans un échantillon donné uniquement parce qu'elles étaient plus âgées. L'asymétrie de la distribution des dates d'éclosion ne disparaît pas au fil du temps, c'est-à-dire que, tant que le taux de mortalité demeure constant, on observe la même tendance dans la distribution quelle que soit la date d'échantillonnage après la fin de la période d'éclosion. Ainsi, la distribution rétrocalculée des dates d'éclosion des larves ne représente pas exactement les dates d'éclosion des survivants selon l'âge, et pourrait être utilisée pour conclure, à tort, que le taux de survie des larves écloses au début de la saison était relativement faible. Le libellé de l'axe de gauche indique les fréquences observées des dates d'éclosion et celui de l'axe de droite indique les fréquences rétrocalculées.

Le taux constant de mortalité supposé dans l'exemple de la figure 10 est manifestement invraisemblable. Une forme quelconque de mortalité sélective selon l'âge ou longueur, c'est-à-dire un taux de mortalité des larves les plus jeunes/les plus petites supérieur à celui des larves les plus âgées/les plus grosses, est davantage probable. Différentes fonctions âge-taux de mortalité sont envisageables, notamment une relation inverse entre le taux de mortalité instantané et l'âge (figure 11). La figure 12 montre l'évolution de la forme de la distribution des dates d'éclosion au fur et à mesure de l'augmentation de la durée entre l'éclosion et le moment de l'échantillonnage. Il est intéressant de noter l'asymétrie initiale de la distribution immédiatement après la fin de la période d'éclosion, imputable au différentiel cumulé élevé de mortalité entre les larves les plus jeunes et les larves les plus âgées. Toutefois, lorsque le taux de mortalité devient très faible (figure 11), le différentiel de mortalité entre celles-ci est considérablement réduit, ce qui donne une distribution des dates d'éclosion reflétant presque exactement celle des dates de production initiale. Les simulations reposant sur la mortalité sélective selon la longueur, plutôt que sur la mortalité sélective selon l'âge, ont donné des résultats similaires, bien que la variance de l'âge par taille ait produit des effets qui se sont manifestés dans plusieurs cohortes quotidiennes. Il est en outre important d'indiquer que la forme de la courbe du taux de mortalité par âge n'est pas pertinente en soi. En effet, le plus important est plutôt le différentiel cumulé de mortalité entre les larves les plus jeunes et les larves les plus âgées de l'échantillon. En l'absence d'autres sources de mortalité, les taux de mortalité par âge constatés sur les âges antérieurs à l'âge le plus jeune de l'échantillon n'ont absolument aucun effet sur la forme de la distribution des dates d'éclosion.

Évolution d'une distribution des dates d'éclosion rétrocalculées au fur et à mesure que l'intervalle de temps entre l'éclosion et l'échantillonnage augmente. Dans cet exemple, l'éclosion s'étend symétriquement sur une période de 30 j (fréquences observées) et il est supposé que le taux de mortalité instantané des larves (M) diminue inversement selon l'âge (figure 11). Des baisses linéaire et exponentielle de M produisent des distributions des dates d'éclosion semblables à celles présentées ici. Il est intéressant de noter l'asymétrie de la distribution rétrocalculée des dates d'éclosion immédiatement après la fin de la période d'éclosion (jour 31). À mesure que l'âge des cohortes quotidiennes augmente et que le M des larves les plus jeunes diminue, le différentiel cumulé de mortalité entre les larves les plus jeunes et les plus âgées diminue, ce qui produit une distribution des dates d'éclosion rétrocalculées de plus en plus symétrique. Le libellé de l'axe de gauche indique les fréquences observées des dates d'éclosion et celui de l'axe de droite indique les fréquences rétrocalculées.

Les résultats de simulation présentés à la figure 12 ont plusieurs conséquences. En premier lieu, il semblerait que la distribution des dates d'éclosion est moins stable, et donc moins fiable, lorsque le taux de mortalité par âge est élevé au moment de l'échantillonnage, étant donné que le différentiel cumulé de mortalité entre les larves les plus jeunes et les plus âgées est élevé aussi. Inversement, la distribution des dates d'éclosion est plus stable lorsque les deux conditions suivantes sont satisfaites : (a) les poissons sont relativement âgés au moment de l'échantillonnage, ce qui fait que le taux de mortalité est stable et faible et (b) la durée de la période de ponte (d'éclosion) est courte, ce qui entraîne un différentiel cumulé minime entre les taux de mortalité des larves les plus jeunes et les plus âgées de la cohorte. En règle générale, on peut établir par approximation la stabilité relative d'une distribution de dates d'éclosion en examinant le rapport entre l'abondance des poissons les plus âgés de l'échantillon et celle des plus jeunes, qui est lui-même une approximation du différentiel cumulé de mortalité des deux âges, comme ci-dessous :

\frac{N_{old}}{N_{young}} = e^{- (\sum_{i = young}^{old} M_{i})}

où N est l'abondance relative dans la population, jeunes et âgés désignent respectivement les âges quotidiens les plus bas et les plus élevés (i) de l'échantillon et M est le taux de mortalité instantané (d^-1). Lorsque le rapport d'abondance est très élevé (p. ex., 0,9), la correction des effets de la mortalité ne modifie pas significativement la distribution des dates d'éclosion. En revanche, un rapport faible (p. ex., 0,05) indique qu'une correction de ces effets s'impose, étant donné que la distribution est instable. Il faut noter que ce rapport n'est utile que lorsque la sélectivité des engins ou l'inégalité de la distribution du poisson n'a pas nui à l'échantillonnage représentatif des deux catégories d'âge.

En théorie, on peut stabiliser une distribution instable des dates d'éclosion en corrigeant le différentiel des taux de mortalité cumulés de la cohorte. En l'absence de correction, l'interprétation de la distribution des dates d'éclosion conduit à des conclusions erronées : plus le différentiel est élevé, plus l'erreur est grande. On doit toutefois noter que la correction de la mortalité n'a rien à voir avec l'interprétation des dates d'éclosion, la correction dépendant de l'âge pour toutes les cohortes et ne servant qu'à mettre les distributions des dates d'éclosion calculées à la même échelle que la production observée. On peut alors interpréter les dates d'éclosion corrigées en fonction des processus de survie/de mortalité par date et cohorte qui ont changé la distribution initiale des dates de production.

Methot (1983) a corrigé le différentiel de mortalité de ses échantillons de poissons juvéniles en multipliant le nombre d'individus par âge par le taux de survie inverse entre l'âge à la capture et l'âge des plus jeunes poissons de l'échantillon. Les estimations du taux de survie qu'il a utilisées avaient été calculées indépendamment. Yoklavich et Bailey (1990) ont apporté des corrections semblables à leurs distributions de dates d'éclosion de larves, mais ils ont été contraints de le faire en utilisant un taux de mortalité hypothétique pour le stade larvaire. L'effet des corrections de la mortalité variait considérablement entre les deux études, démontrant clairement la difficulté à analyser des distributions de dates d'éclosion pour des larves connaissant un taux de mortalité élevé. Dans l'étude de Methot (1983), le taux de mortalité du stade juvénile est relativement faible et la correction de la mortalité a entraîné des différences relativement faibles entre les formes des distributions des dates d'éclosion corrigées et brutes. À l'opposé, le différentiel de mortalité des larves jeunes et âgées des échantillons de Yoklavich et Bailey (1990) est important et la distribution corrigée s'écarte nettement de la distribution brute. L'utilisation d'une autre courbe de mortalité pourrait avoir changé différemment la distribution des dates d'éclosion.

Il est rarement possible de corriger les distributions de dates d'éclosion instables sans ambiguïté, car en général, aucune estimation du taux de survie calculée indépendamment, comme celles de Methot (1983), n'est disponible. En outre, en présence de taux de mortalité élevés et imprévisibles, comme c'est le cas pour de nombreuses larves pélagiques, la correction de la mortalité reposant sur des courbes de mortalité moyenne ou hypothétique peut très bien conduire à des distributions des dates d'éclosion qui ne représentent pas la réalité. Par conséquent, il est préférable d'analyser les dates d'éclosion d'un stade du cycle biologique caractérisé par un taux de mortalité faible et stable, de sorte que la correction de la mortalité ait peu d'incidence sur la forme de la distribution. Dans les cas où une correction de la mortalité influente doit être appliquée, la forme de la correction doit être soigneusement justifiée.

Si la correction de la mortalité est un moyen de modifier une distribution instable des dates d'éclosion, il en existe peut-être un autre (non encore testé) permettant d'éviter complètement l'instabilité. Comme il a été indiqué auparavant, on détermine généralement la production de larves nouvellement écloses (ou d'œufs) par échantillonnage séquentiel pendant toute la période d'éclosion des œufs. En principe, alors, il devrait être possible de surveiller l'abondance d'une cohorte donnée, ou de plusieurs cohortes, par échantillonnage séquentiel pendant un intervalle de même durée que la période de production. Les distributions des dates d'éclosion de chaque échantillon pour une plage d'âges donnée pourraient alors être additionnées pour toutes les dates, en vue d'obtenir une distribution unique dans laquelle chaque cohorte quotidienne a été échantillonnée pour une même plage d'âges. Ainsi, puisqu'il n'y aurait aucune mortalité différentielle cumulée entre les cohortes quotidiennes, il serait inutile de corriger la mortalité. Prenons par exemple la production de larves nouvellement écloses dans un petit lac. Supposons que la production est surveillée quotidiennement pendant toute la période d'éclosion s'étalant sur 30 j (jours 0 à 30). Si un nouvel échantillonnage est effectué quelque 50 j plus tard (jour 80) en vue d'établir l'abondance des juvéniles, toute mortalité différentielle cumulée des poissons de 50 j et de ceux de 80 j rend asymétrique la distribution calculée des dates d'éclosion. Toutefois, si tous les juvéniles sont échantillonnés quotidiennement entre le jour 50 et le jour 80, la somme des distributions des dates d'éclosion des poissons de 50 à 80 j présents dans chaque échantillon quotidien devrait représenter précisément la distribution des dates d'éclosion de toutes les cohortes écloses après 50 j. On doit noter que ce n'est pas une simple addition de toutes les distributions des dates d'éclosion pendant la période d'échantillonnage, étant donné que les poissons de moins de 50 j ne sont pas inclus dans les calculs (p. ex., seuls les poissons de 50 j présents dans l'échantillon de juvéniles prélevé le jour 50 sont inclus, malgré le fait que l'échantillon contient des poissons de 20 à 50 j). L'absence de sélectivité des engins pour certains âges ou longueurs et d'immigration dans la zone d'échantillonnage ou d'émigration de celle-ci de poissons de certains âges ou longueurs sont les hypothèses clés de cette méthode. En outre, la périodicité de l'échantillonnage détermine le niveau de résolution auquel la distribution finale des dates d'éclosion peut être interprétée.

Il est possible de combiner l'échantillonnage séquentiel sur une base autre que quotidienne (p. ex., hebdomadaire) avec une forme de correction de la mortalité pour obtenir une distribution corrigée des dates d'éclosion des larves. Une telle procédure devrait probablement diminuer la correction de la mortalité nécessaire dans le cas d'un échantillon unique, tout en étant logistiquement plus facile à exécuter qu'un échantillonnage quotidien. Toutefois, à notre connaissance, personne n'a encore établi de distribution des dates d'éclosion par échantillonnage séquentiel quotidien, et encore moins par échantillonnage séquentiel combiné avec une correction de la mortalité.

L'application la plus commune de l'analyse des dates d'éclosion concerne l'identification des fractions favorisées ou appauvries d'une classe d'âge, suivie de la corrélation entre les fractions perturbées et les signaux environnementaux dominants. Citons comme exemples de ces signaux notamment les périodes de mélange accru résultant de tempêtes, de remontée des eaux, de pertes par advection de la zone de relevé, de disponibilité faible ou élevée de nourriture et d'abondance faible ou forte de prédateurs. La plupart de ces corrélations conviennent mieux à certains stades du cycle biologique (p. ex., larves après résorption du sac vitellin). Il est toutefois important de noter que l'analyse des dates d'éclosion ne peut pas servir à déterminer la date ou l'âge auxquels la distribution de ces dates a été perturbée. En effet, les forces qui ont favorisé ou appauvri une partie de la cohorte peuvent avoir été actives juste après l'éclosion ou des semaines plus tard, juste avant l'échantillonnage, et l'analyse des dates d'éclosion ne permet pas de distinguer ces deux possibilités. Par conséquent, il est difficile d'associer sans ambiguïté un signal environnemental en particulier à un changement de la distribution des dates d'éclosion étant donné qu'il aurait pu se produire à tout moment entre l'éclosion et l'échantillonnage. En principe, il est possible d'utiliser un échantillonnage séquentiel pour cerner les dates auxquelles le changement a pu se produire. Toutefois, comme il a été mentionné plus haut, la valeur de l'analyse des dates d'éclosion est sujette à caution lorsque les taux de mortalité sont élevés, ce qui peut malheureusement très bien correspondre au stade du cycle biologique étudié. Bien entendu, certaines sources de mortalité sont plus susceptibles de toucher des stades particuliers du cycle biologique plutôt que d'autres; ainsi, la sortie par advection d'une zone favorable est plus susceptible d'entraîner la mort des très jeunes larves, encore peu capables de se déplacer, que des juvéniles plus âgés. À l'inverse, l'absence de grosses proies peut entraîner une mortalité élevée chez les juvéniles sans avoir d'effet net sur les jeunes larves. Par conséquent, bien qu'une distribution stable des dates d'éclosion puisse montrer clairement la survie accrue de certaines cohortes quotidiennes, il n'est pas nécessairement facile de déterminer les sources de cette survie meilleure ou l'âge des larves touchées.

Estimation de la mortalité

Depuis quelques années, la technique de détermination de l'âge quotidien sert de plus en plus à établir le taux de survie de poissons de moins d'un an. La possibilité de mesurer l'abondance et le taux de survie à un âge donné représente une nette amélioration par rapport à l'estimation du taux de mortalité d'après la seule taille, car la taille des jeunes poissons n'est pas une bonne mesure de leur âge et une catégorie de taille donnée correspond souvent à plusieurs classes d'âges. Les mesures de l'abondance à un âge donné offrent la possibilité d'étudier les causes subtiles qui nuisent à la survie des jeunes poisons. Citons quelques études récentes reposant sur la détermination de l'âge quotidien : Houde (1989), Owen et al. (1989), Athossaini et al. (1989), Fortier et Gagné (1990) et Pepin (1991). Elles portent principalement sur l'attribution de la mortalité à diverses causes pendant les premiers stades du cycle biologique. Cette liste partielle ne montre qu'un petit échantillon des types d'études en cours.

Concepts fondamentaux de l'estimation de la mortalité

La baisse de l'abondance d'une cohorte pendant une période déterminée permet d'estimer le taux de mortalité. Une cohorte est un groupe fermé ou limité d'individus dont l'abondance, après leur naissance, ne peut que diminuer. Le graphique (figure 13) de l'abondance d'une cohorte révèle que l'abondance initiale (N0) est plus élevée à l'éclosion, puis diminue au fur et à mesure que des éléments meurent notamment en raison d'une pénurie prolongée de nourriture, de la prédation, de maladie ou du transport par advection vers des zones où leur survie est réduite. Avant la conception de la méthode de détermination de l'âge quotidien, le taux de mortalité était estimé par des expériences en enclos ou des observations de la diminution des effectifs de classes de longueurs de plus en plus grandes sur le terrain. Cette démarche pose cependant une difficulté : les sources de mortalité sont souvent ponctuelles (p. ex., événements d'advection, pénurie de nourriture, présence de prédateurs) et ne peuvent pas être distinguées des mesures fondées sur la longueur. Étant donné qu'en général, la longueur n'est pas un indicateur particulièrement pertinent de l'âge, les méthodes fondées sur celle-ci ne permettent pas de suivre des cohortes correctement définies et donnent donc des résultats souvent trop peu précis pour être utiles.

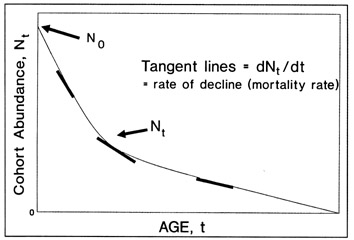
FIGURE 13. Représentation théorique de l'abondance d'une cohorte tout au long de sa vie. Les trois droites tangentes en gras indiquent la baisse de la pente, le taux absolu de mortalité au moment t, au fur et à mesure que l'âge des poissons augmente. Dans ce modèle, Z (taux instantané de mortalité) est constant, bien que cela ne soit pas requis.

On peut illustrer les profils de mortalité à l'aide de courbes de survie théorique (voir figure 14, d'après Slobodkin 1961). Ces courbes de survie permettent de modéliser la forme du déclin de l'abondance d'une cohorte donnée au fil de sa vie. Les courbes de type III se prêtent habituellement mieux à la modélisation des premiers stades du cycle biologique des poissons. En général, la mortalité naturelle est extrêmement élevée aux stades des œufs et des larves (p. ex., 2 à 10 % par jour chez les plies et les clupéidés - Cushing 1975; Smith 1985), diminue rapidement pendant le stade juvénile (Dahlberg 1979; Crecco et al. 1983), se stabilise relativement durant le stade adulte et enfin peut augmenter chez les individus âgés (Vetter 1988). La courbe la plus connue, soit celle de type III, est représentée par l'équation suivante, souvent utilisée pour la fonction exponentielle négative :

(28)

N_{t} = N_{0} e^{- Z t}

En reformulant l'équation 28 et en transformant les données en logarithmes, on peut calculer Z, soit le taux de mortalité instantané total entre le moment 0 et t. On doit noter que, par convention, Z est un nombre positif.

(28)

Z = \frac{- ln (\frac{N_{t}}{N_{0}})}{t}

La relation représentée repose sur le calcul du taux de mortalité instantané. Celui-ci n'est pas aussi intuitif à comprendre que le taux de survie réel, S, où S = N_t / N₀, ou le taux de mortalité réel, A, où A = 1 - S = 1 - N_t / N₀. Ces taux finis, souvent utilisés pour exprimer le taux de mortalité ou de survie des larves, ne se prêtent pas à la séparation des composantes de la mortalité, étant donné qu'il n'est pas facile de les comparer lorsque les unités de temps sont différentes (p. ex., un taux de mortalité de 10 % par année n'équivaut pas à deux périodes de mortalité de 5 % pour une période de 6 mois). À l'inverse, les taux instantanés de mortalité s'additionnent facilement.

FIGURE 14. Courbes de survie hypothétiques (courbes de Slobodkin 1961 modifiées). Une courbe de type I montre un faible taux de mortalité à la fin de la vie, celle de type II montre un taux de mortalité absolu égal à tous les stades du cycle biologique tandis que celle de type III est fréquemment utilisée pour modéliser le taux de mortalité de poissons étant donné qu'elle indique qu'une proportion constante de la cohorte meurt au fil du temps.<br /> <br />Cliquer sur la vignette pour agrandir la figure.

Le taux de mortalité instantané varie selon le ratio des niveaux d'abondance, ce ratio étant tout simplement la proportion de survivants. De là, l'équation ci-dessus indique que la mortalité touche une proportion constante de la population au fil du temps. Disons que 10 % des poissons restants meurent chaque jour. Étant donné que ce pourcentage constant est défalqué d'une abondance en baisse constante, le nombre absolu de poissons mourant à chaque période diminue en fait au fil du temps : 10 % de 100 poissons représentent 10 poissons morts, 10 % des 90 restants en représente 9 et ainsi de suite.

Le taux de mortalité totale (Z) est habituellement calculé selon la formule Z = M + F, où M est le taux instantané de mortalité naturelle et F le taux instantané de mortalité par pêche. Même chez les espèces faisant l'objet d'une pêche commerciale ou récréative, la pêche ne les vise habituellement pas pendant la première année de leur vie. Le taux de mortalité totale durant cette première année est donc égal au taux de mortalité naturelle (Z = M). En réalité, M change probablement pendant les divers stades du cycle biologique; il est donc préférable de le représenter comme suit :

M = \sum_{i = 1}^{n} M_{i}

où n = nombre de stades du cycle biologique inclus dans l'analyse. Dans la plupart des cas, M est considéré comme une moyenne des M_i.

Le taux instantané de mortalité est souvent très élevé au début du cycle biologique, puis diminue au fil du temps. Une courbe où le taux de mortalité change d'un stade à l'autre est donc la plus appropriée pour le représenter (figure 15). Lorsque l'abondance chute aussi rapidement, l'équation exponentielle négative ne correspond pas très bien aux données réelles. Une autre méthode consiste à estimer le taux de mortalité pendant seulement une partie du cycle biologique. Si la fonction exponentielle négative donne toujours un mauvais ajustement, des fonctions mathématiques plus complexes et moins connues peuvent être appliquées aux données. Neilson et al. (1989) ont utilisé la fonction de Weibull, employée par les ingénieurs dans la prévision des pannes de matériel, pour modéliser des données sur la mortalité des adultes, tandis que Lo et al. (1989) ont employé la fonction de Pareto pour simuler la mortalité chez les larves d'anchois. Le test du chi carré permet d'évaluer la qualité de l'ajustement de toutes ces fonctions. Il est toutefois souvent préférable d'utiliser la fonction exponentielle, plus connue, pour modéliser les taux de mortalité. L'utilisation d'autres fonctions présente en effet plusieurs inconvénients : elles sont peu connues, les résultats sont difficilement comparables à d'autres travaux et l'estimation des intervalles de confiance est plus difficile.

Courbe de survie hypothétique lorsque le taux de mortalité change d'un stade à l'autre du cycle biologique.

Il est théoriquement très simple d'estimer le taux de mortalité. On mesure l'abondance d'une cohorte à un premier moment (N₀), puis plus tard (N_t), de façon à obtenir toute l'information requise pour résoudre l'équation 28. En réalité, il peut se révéler assez difficile de calculer précisément ces estimations de l'abondance, particulièrement pour les stades larvaires et juvéniles. Lorsque l'échantillonnage est limité, comme c'est souvent le cas, la variance et les intervalles de confiance sont grands et l'estimation de l'abondance peut être très éloignée de sa valeur réelle. L'évitement des engins par les gros poissons est problématique notamment pour le calcul des taux de mortalité (voir Butler, dans la publication citée en haut de la page). En outre, l'inégalité de la répartition des larves, en particulier chez les espèces marines, peut causer des estimations absurdes de Z lorsque, à cause de la variabilité de l'échantillonnage, l'abondance estimée des stades avancés est plus élevée que celle du début du cycle biologique (N_t > N₀).

Méthodes de calcul du taux de mortalité

On désigne habituellement par cohorte tous les poissons issus des œufs produits par une population pendant une année donnée. Comme il est maintenant possible de déterminer l'âge quotidien, ce terme peut également désigner les « cohortes » quotidiennes ou hebdomadaires produites au cours d'une période de ponte. Auparavant, ces cohortes au sein d'une saison étaient identifiées à l'aide de méthodes fondées uniquement sur la longueur. Cependant, il est souvent impossible d'attribuer ces cohortes à des classes d'âge en suivant la progression des modes de longueur au fil du temps à cause de l'absence d'impulsions de ponte différenciées chez de nombreuses espèces (aucun mode distinct n'est produit). Même en cas d'impulsions de ponte, la variabilité de la croissance entraîne la présence de plusieurs classes d'âge (quotidiennes) dans chaque catégorie de longueur peu après l'éclosion. Le dénombrement des accroissements journaliers permet toutefois d'estimer directement le taux de mortalité à un âge donné.

Bien que certains scientifiques, à la recherche de preuves de la mortalité dans l'année, ont tout simplement comparé des larves écloses tôt à des larves écloses tard dans la saison, d'autres groupements temporels sont possibles (p. ex., hebdomadaires, bimensuels et même quotidiens). L'erreur de mesure au moment de la lecture et de la détermination de l'âge est une source de variance dans ces groupements (voir Neilson, dans la publication citée en haut de la page). L'âge attribué est en fait une estimation susceptible de varier de plusieurs jours, même sans biais. On peut réduire la variabilité de l'estimation de l'âge en regroupant les jeunes poissons en cohortes de plusieurs jours au cours de la saison du frai (voir Crecco et Savoy 1985, pour une explication de leur méthode de regroupement en cohortes).

Les méthodes d'estimation du taux de mortalité se divisent en méthodes directe et indirectes (Krebs 1972). La méthode directe repose sur le marquage et la recapture de membres d'une cohorte en vue de suivre le déclin du nombre d'individus marqués au fil du temps. Les techniques indirectes sont les suivantes : (1) l'analyse de courbes de capture, (2) les corrélations entre la mortalité naturelle et d'autres paramètres du cycle biologique et (3) l'estimation du taux de mortalité due à la prédation (Vetter 1988). De toutes ces méthodes, la méthode d'analyse des courbes de capture est la plus souvent utilisée pour les larves et les juvéniles, les deux autres méthodes indirectes étant rarement, voire jamais, appliquées aux jeunes poissons. Après une brève description des méthodes de marquage et de recapture, les méthodes d'analyse des courbes de capture seront discutées en détail.

Marquage et recapture

Les méthodes de marquage et de recapture de poissons adultes servent couramment à établir les sources de la mortalité (Brownie et al. 1985; Burnham et al. 1987), mais rarement à estimer le taux de mortalité de très jeunes poissons. Le marquage des jeunes poissons peut être fait en masse (les mêmes marques sont utilisées pour tous les individus) ou avec des étiquettes identifiant chaque poisson. Les petits poissons et les très jeunes poissons étant délicats et difficiles à manipuler, les otolithes sont habituellement marqués en masse à l'aide de produits chimiques (Hettler 1984; Schmidt 1984; Tsukamoto 1985). Si le marquage par lot empêche de suivre chaque individu, il est en revanche très adapté pour mesurer les changements de l'abondance grâce au grand nombre d'individus marqués. Les juvéniles sont plus gros, plus faciles à manipuler et assez résistants pour porter une étiquette, par exemple une micromarque magnétisée codée. Le marquage individuel peut servir à rechercher des différences plus subtiles entre les taux de mortalité de plusieurs groupes (au sein de cohortes ou entre elles) et des interactions avec la croissance et/ou le lieu, mais il est généralement plus difficile de marquer un grand nombre de poissons.

Plusieurs hypothèses importantes doivent être satisfaites avant d'utiliser les méthodes de marquage et de recapture pour estimer l'abondance et le taux de mortalité d'une population, notamment : (1) les poissons étiquetés sont représentatifs de la population pour laquelle de l'information sur la mortalité est recherchée, (2) aucune émigration des poissons étiquetés ne se produit, (3) le nombre exact de poissons étiquetés remis à l'eau est connu précisément, (4) aucune étiquette n'est perdue ou incorrectement lue, (5) l'étiquetage n'a pas d'effet sur les taux de survie et (6) le sort de chaque poisson étiqueté est indépendant des autres individus étiquetés (Brownie et al. 1985; Burnham et al. 1987). Aucune de ces hypothèses ne s'applique seulement aux poissons dont les otolithes ont été marqués, bien que la tétracycline ait été signalée comme capable d'accroître (Tsukamoto 1985) ou de réduire (McFarlane et Beamish 1987) la survie des poissons étiquetés par rapport aux poissons témoins.

Quatre principaux obstacles peuvent entraver l'utilisation d'otolithes marqués pour estimer le taux de mortalité de larves de poisson : (1) la mortalité due à la manipulation et au marquage, (2) des taux de mortalité intrinsèquement élevés, ce qui signifie que de très grands nombres de poissons doivent être marqués pour pouvoir en recapturer, (3) l'absence de pêches commerciales et sportives visant des jeunes poissons, exigeant que le chercheur recapture les poissons marqués et (4) les biais introduits par l'évitement des filets et les changements d'engins. Comme dans le cas des hypothèses sous-jacentes, ces limites ne s'appliquent pas seulement aux poissons aux otolithes marqués et se retrouvent souvent dans d'autres études recourant au marquage et à la recapture de jeunes poissons.

Le taux de mortalité calculé d'après les résultats d'une étude de marquage et de recapture représente simplement la baisse du nombre de poissons recapturés au fil du temps. L'équation 28 peut être reformulée de façon à refléter le taux de mortalité estimatif provenant d'études d'étiquetage, ce qui donne :

N_{r t} = N_{r 0} e^{- Z t}

où N_rt est le nombre de poissons recapturés au moment t et N_r0 le nombre de poissons étiquetés et remis à l'eau. Étant donné que le nombre de poissons recapturés peut varier, il est conseillé d'effectuer des prélèvements à des dates différentes afin de stabiliser l'estimation du taux de mortalité (voir Gulland 1983, p. 110-115, pour une description de cette méthode).

Analyse des courbes de capture

L'analyse des courbes de capture est la méthode indirecte d'estimation de la mortalité la plus fréquente. Bien qu'elle soit appliquée principalement à des poissons adultes, elle se révèle aussi pertinente pour les premiers stades du cycle biologique (Crecco et al. 1983; Essig et Cole 1986). L'estimation de la mortalité des larves de poisson se fonde presque exclusivement sur l'analyse des courbes de capture, bien que ce ne soit pas toujours explicitement indiqué dans les méthodes des articles sur le sujet. Krebs (1972) prévient que les méthodes indirectes reposent sur l'acceptation de certaines hypothèses et que ces dernières doivent être valides pour que ces méthodes puissent être utilisées correctement. Cette recommandation s'applique particulièrement à l'analyse des courbes de capture. Elles représentent la fréquence des tailles ou des âges du poisson capturé (figure 16). Mais comme la taille est souvent un mauvais indicateur de la cohorte d'origine (May 1974; Warlen 1981), il est préférable d'utiliser l'âge établi par dénombrement des accroissements journaliers. L'abondance par âge diminuant habituellement de façon exponentielle, la pente ou Zt (exprimée comme un nombre positif par convention) devient le taux de mortalité à un moment donné. La valeur de Z peut être estimée soit par régression non linéaire des données brutes ou par transformation logarithmique des données sur l'abondance (Ricker 1975). Cette dernière donne habituellement une courbe plus ou moins droite à pente négative, qui peut ensuite être ajustée par régression ordinaire des moindres carrés (voir Robson et Chapman 1961; Ricker 1975; Draper et Smith 1981). L'abondance des plus jeunes classes d'âge (figure 16) est souvent inférieure à l'abondance maximale, car l'engin d'échantillonnage n'est pas en mesure d'en capturer suffisamment, ce qui se reflète par une partie gauche ascendante de la courbe. Il faut ignorer cette dernière lorsqu'on ajuste la courbe de régression et n'utiliser dans l'analyse que les données sur l'abondance décroissante. La valeur absolue de la pente de la courbe de régression ajustée est une estimation de Z qui, dans le cas des premiers stades non exploités du cycle biologique, est égale au taux de mortalité naturelle ou M.

Représentation simplifiée d'une courbe de capture. Les données estimées d'abondance sont transformées en logarithme. La représentation incomplète des plus jeunes poissons dans les prises donne un sens ascendant à la partie gauche de la courbe. Seule la partie droite est utilisée pour estimer le taux de mortalité.<br /> <br />Cliquer sur la vignette pour agrandir la figure.

Il existe deux types de courbes de capture : par âge et par cohorte. Pour les adultes, on utilise souvent la première qui repose sur le prélèvement d'un seul échantillon à un moment donné. Elle ne peut pas servir, en revanche, à estimer en saison le taux de mortalité de cohortes des premiers stades du cycle biologique. L'hypothèse sous-jacente extrêmement restrictive s'appliquant à cette courbe de capture veut que « les groupes pour lesquels des données ont été recueillies doivent être en état d'équilibre l'un par rapport à l'autre » (Vetter 1988), ce qui signifie que l'abondance de toutes les classes d'âge (i) au début de leur vie, soit Noi, doit être égale. En revanche, l'abondance relative des larves et des juvéniles à un moment donné dans le temps dépend aussi du niveau de ponte, qui varie aussi dans le temps. La quantité d'œufs (de larves) produits pendant la saison du frai suit souvent une distribution normale ou peut-être même une distribution polymodale, ce qui contredit l'hypothèse d'abondance initiale égale et uniforme de chaque cohorte pendant la saison du frai.

La courbe de capture par cohorte, semblable à une analyse de tables de survie, est privilégiée pour estimer le taux de mortalité en saison des premiers stades du cycle biologique. Elle repose sur l'échantillonnage séquentiel de l'abondance d'un seul groupe bien distinct pendant le stade du cycle biologique étudié (figure 16). Dans le cas des larves, cela pourrait être la production d'une seule semaine échantillonnée pendant les semaines suivantes (voir Crecco et Savoy 1985) ou, plus simplement, une estimation à deux points du taux de mortalité fondé sur l'abondance d'une cohorte distincte à deux âges différents. Un taux de mortalité des âges échantillonnés non constant produit une courbe de capture incurvée. Dans ce cas, on peut estimer le taux de mortalité pour certaines parties du cycle de la cohorte, mais on n'obtient pas de taux de mortalité unique.

La courbe de capture par âge est assujettie à plusieurs hypothèses qui doivent être satisfaites, nommément : (1) les échantillons sont représentatifs de l'ensemble de la population (c'est-à-dire habituellement qu'ils ont été prélevés au hasard); (2) la population n'est pas susceptible de migrer ou d'être échantillonnée différemment par l'engin selon l'âge (la capturabilité ou q est constante) et (3) les cohortes doivent être reconnaissables et définies de manière fiable (Vetter 1988). Souvent, plusieurs de ces hypothèses ne sont pas respectées aux premiers stades du cycle biologique à cause de changements apportés au comportement, à l'habitat et à l'engin utilisés pour l'échantillonnage. Par exemple, comme les grosses larves peuvent plus facilement éviter les filets (deuxième hypothèse, soit une capturabilité constante), une baisse de l'abondance peut être imputable à la mortalité ou à l'évitement du filet. La sélectivité d'un filet peut aussi résulter de changements du comportement diurne (May 1974), comme le début de migrations nycthémérales lorsque l'âge des larves augmente. Ce changement d'habitat, par exemple du stade planctonique au stade benthique, peut aussi coïncider avec le déclenchement du rassemblement en bancs ou de la territorialité qui, à son tour, est susceptible d'agir sur la densité du poisson et sa capturabilité. Par conséquent, la densité des larves n'est pas directement comparable à la densité des juvéniles. Dans ce cas, les courbes de survie doivent être divisées en phases d'âge/de longueur et le taux de mortalité, établi séparément pour chaque phase. Il est alors possible de comparer la pente des courbes de capture ou Z entre phases.

En règle générale, l'abondance réelle ou N_t n'est pas incluse dans les courbes de capture. On estime plutôt une mesure de substitution des prises par unité d'effort ou C_t/f. L'équation du volume des prises est la suivante :

C_{t} = q f N_{t}

où f est l'effort d'échantillonnage et q le coefficient de capturabilité. Elle peut être reformulée pour obtenir le volume des prises par unité d'effort, comme suit :

\frac{C_{t}}{f} = q N_{t}

Autrement dit, on considère que les prises par unité d'effort sont proportionnelles à l'abondance. L'équation du taux de mortalité peut être reformulée pour donner ln {Nt/N0} = -Zt, en matière de prises par unité d'effort, comme suit :

\frac{\frac{C_{t}}{f_{t}}}{\frac{C_{0}}{f_{0}}} = \frac{q_{t} N_{t}}{q_{0} N_{0}} = \frac{q_{t} f_{t}}{q_{0} f_{0}} e^{- Z t} = \frac{q_{t}}{q_{0}} e^{- Z t}

Il est relativement facile de normaliser l'effort d'échantillonnage et donc de rendre f₀ égal à f_t. On suppose souvent que q₀ et q_t sont égaux aussi ou que toute différence dans q est attribuable à l'évitement et à l'évasion du filet. Des facteurs de correction sont utilisés pour essayer d'égaliser les fréquences d'abondance. Si l'hypothèse de capturabilité égale n'est pas satisfaite, les estimations du taux de mortalité tirées des courbes de capture ne reflètent pas la réalité.

À cause des changements de capturabilité imputables à la taille, il peut être difficile d'établir les taux de mortalité absolus aux premiers stades du cycle biologique, même lorsqu'on peut déterminer l'âge quotidien. Hoenig et al. (1990) ont donc conçu une méthode pour comparer le taux de survie relatif de deux cohortes de poissons produites pendant la même saison (par exemple, au début et à la fin d'une saison). Cette méthode est utilisable lorsque la capturabilité, ou q, des deux groupes n'est pas égale. On peut aussi le faire lorsque la microrépartition est marquée et que le ratio estimé des niveaux d'abondance absolue ou N_t/N₀ est dénué de sens (> 1). Hoenig et al. (1990) ont utilisé le ratio des prises de larves produites au début et à la fin de la saison échantillonnée à un moment donné dans le temps ou t. L'équation du ratio est R_t = C_Lt/C_Et, où C_Lt et C_Et sont respectivement les prises issues des cohortes produites au début et à la fin de la saison. Les poissons sont échantillonnés deux fois, mais de préférence plus souvent, et le logarithme de R_t est défini par t. La pente de cette droite est une estimation de la différence des taux de mortalité instantanés des deux groupes de poissons. Cet estimateur du ratio repose sur l'hypothèse (1) qu'il n'y a ni immigration ni émigration dans la zone étudiée et (2) que le ratio des coefficients de capturabilité ou q_t/q₀ des groupes ne change pas pendant la période étudiée. Cette méthode peut servir à comparer le taux relatif de survie de divers groupes, comme des larves produites au début et à la fin d'une saison, même si le nombre produit à ces deux moments ou N_0i n'est pas identique. Elle peut en outre être utile lorsque l'hypothèse de capturabilité égale ne peut pas être prouvée. On doit toutefois noter que la deuxième hypothèse, soit un ratio constant des coefficients de capturabilité, est difficile à mettre à l'essai.

Date de modification :: 2019-01-17

Sélection de la langue

Recherche

Analyse des données sur les microstructures d'otolithes

Raccourcis vers les principales sections :

L'information de la page doit être citée comme suit :

Introduction

Estimation de l'âge

Conversion des dénombrements d'accroissements en estimations de l'âge

Exactitude et précision

Clés âge-longueur

Estimation de l'âge par intégration numérique de largeurs d'accroissements journaliers

Modèles de croissance

Modèles empiriques

Modèles de régression linéaire simples

Modèles de croissance curviligne

Modèles de croissance âge-température

Erreurs communes d'ajustement des modèles

Rétrocalcul de la croissance

Problèmes des rétrocalculs classiques de la croissance

Rétrocalculs reposant sur l'algorithme du point d'intersection biologique

Rétrocalculs reposant sur des algorithmes multivariés

Rétrocalcul de la croissance récente

Croissance et environnement

Analyse des dates d'éclosion

Estimation de la mortalité

Concepts fondamentaux de l'estimation de la mortalité

Méthodes de calcul du taux de mortalité

Marquage et recapture

Analyse des courbes de capture